跳转至

Applied Deep Learning 2024

课程说明

Backpropagation 效率地计算大量参数

符号说明

符号 含义 说明
\(a_i^l\) output of a neuron 第\(l\)层第\(i\)个神经元的激活输出，是经过激活函数之后的输出，a是激活actviation的首字母
\(a^l\) output vector of a layer 第\(l\)层所有神经元的输出组成的向量
\(z_i^l\) input of activation functiion 第\(l\)层第\(i\)个神经元的加权输入（又叫 pre-activation），作为激活函数的输入
\(z^l\) input vector of activation function for a layer 第\(l\)层所有神经元的加权值
\(w_{ij}^l\) a weight 第\(l-i\)层的第\(j\)个神经元到第\(l\)层\(i\)个神经元的权重
\(w^l\) a weight matrix 第\(l\)层的权重矩阵
\(b_i^l\) a bias 第\(l\)层第\(i\)的神经元的偏置
\(b^l\) a bias vector 第\(l\)层所有神经元组成的向量

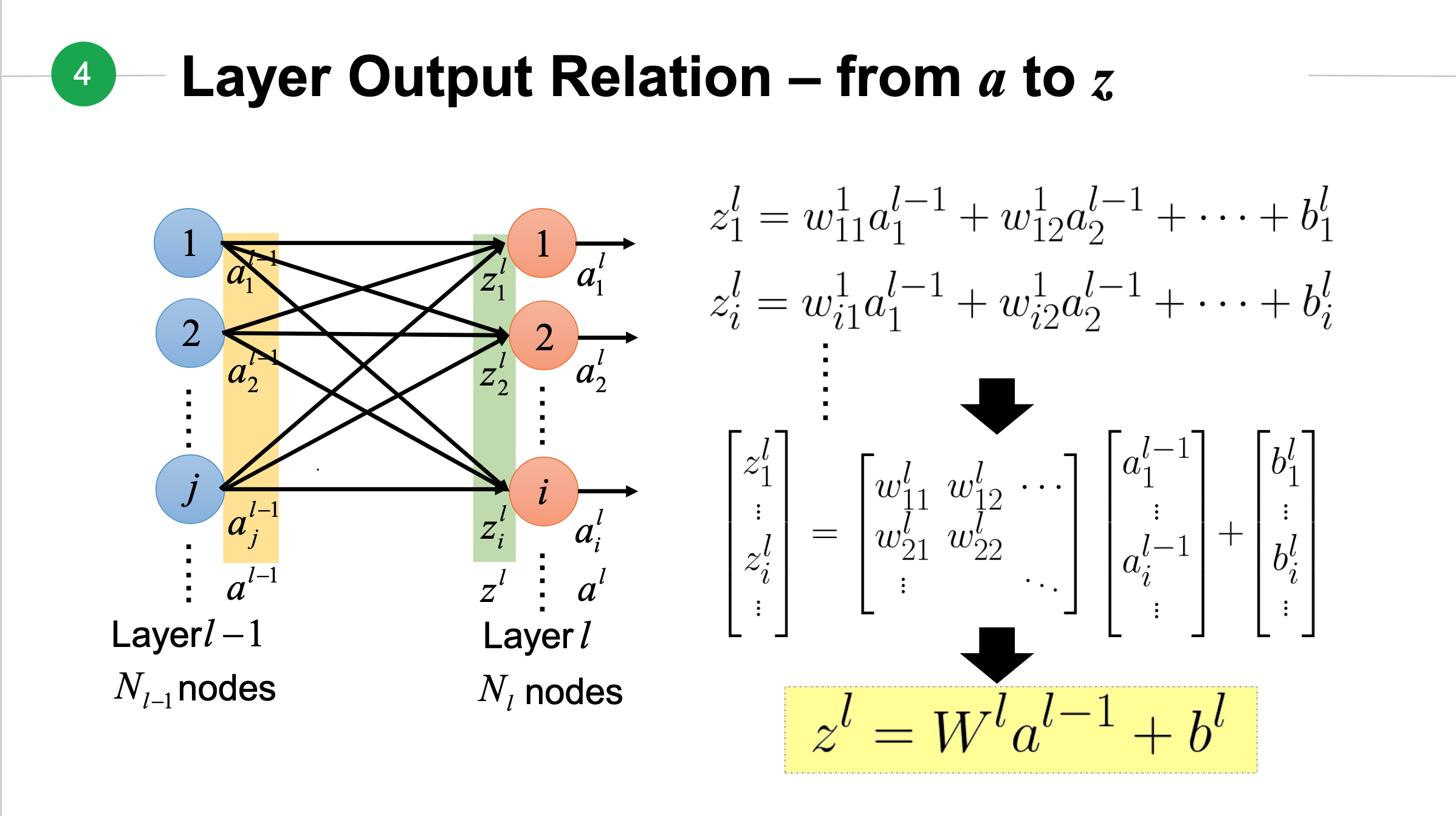
神经元输出

下图是从第\(l-1\)层的\(a\)到第\(l\)层\(z\)的关系，其中\(l-1\)层有\(N_{l-1}\)个节点(node)，第\(l\)层有\(n_l\)个节点：

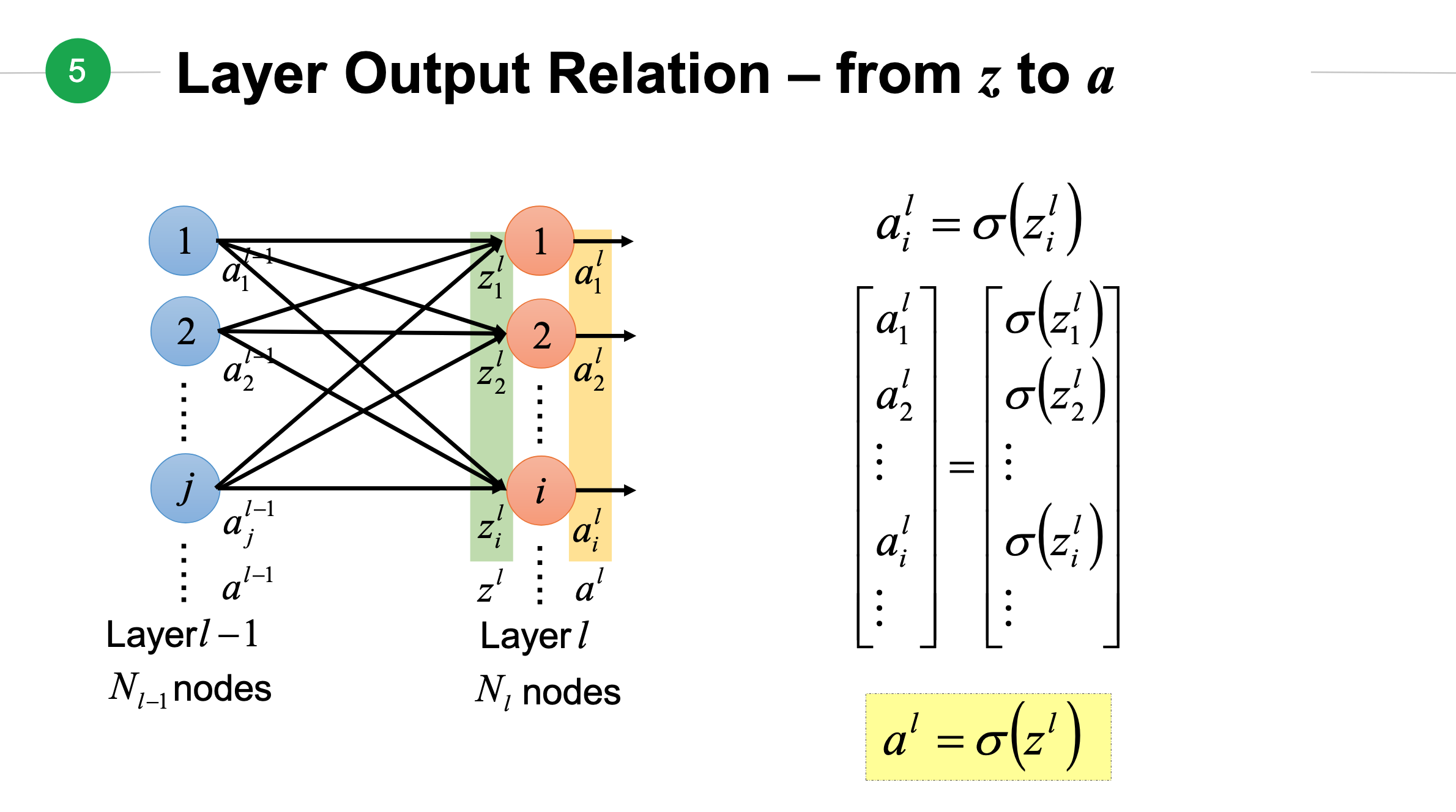
如果将上面得到\(z\)放入到激活函数中将会得到从\(z\)到\(a\)的结果：

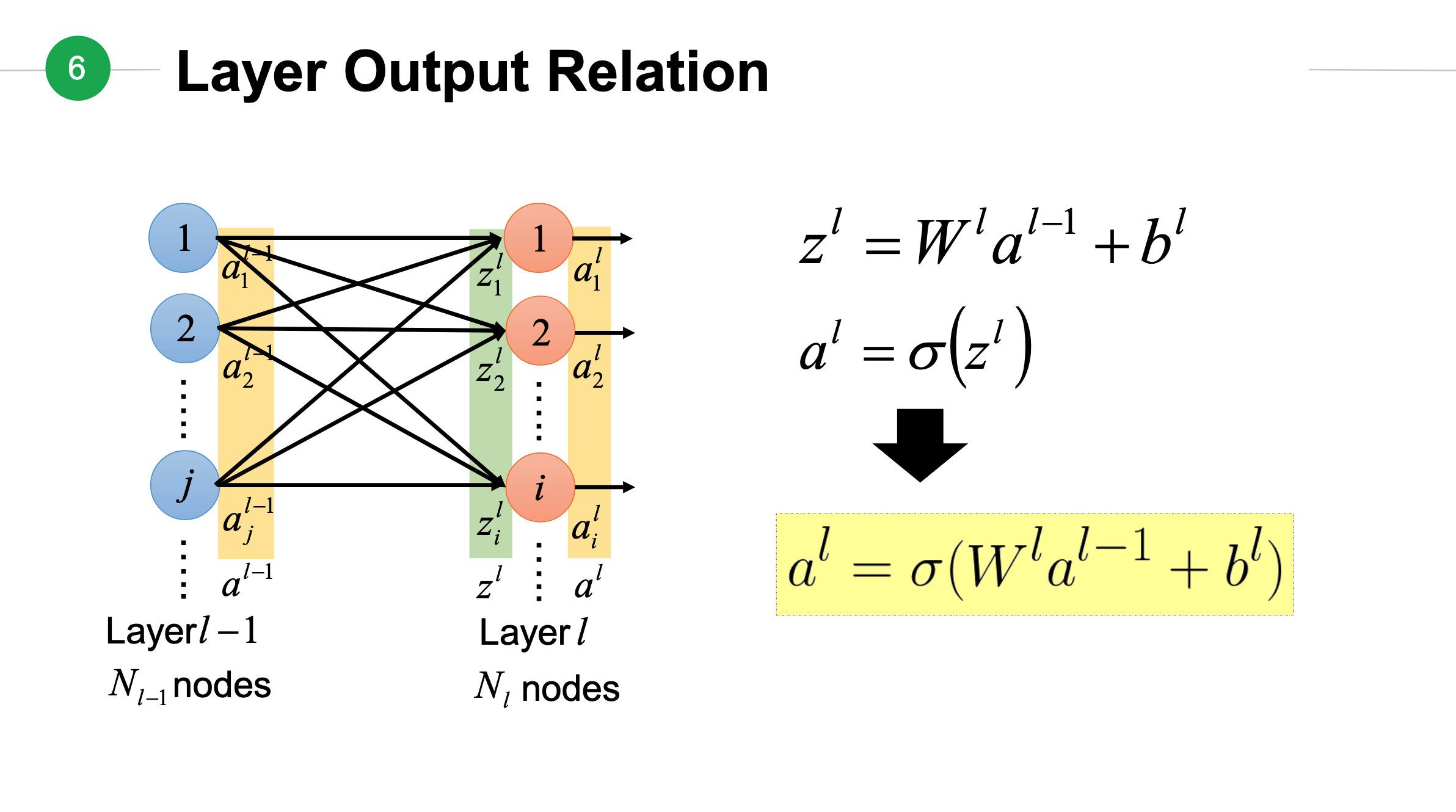
上面两个输出整合在一起，构成第\(l\)层神经元输出：

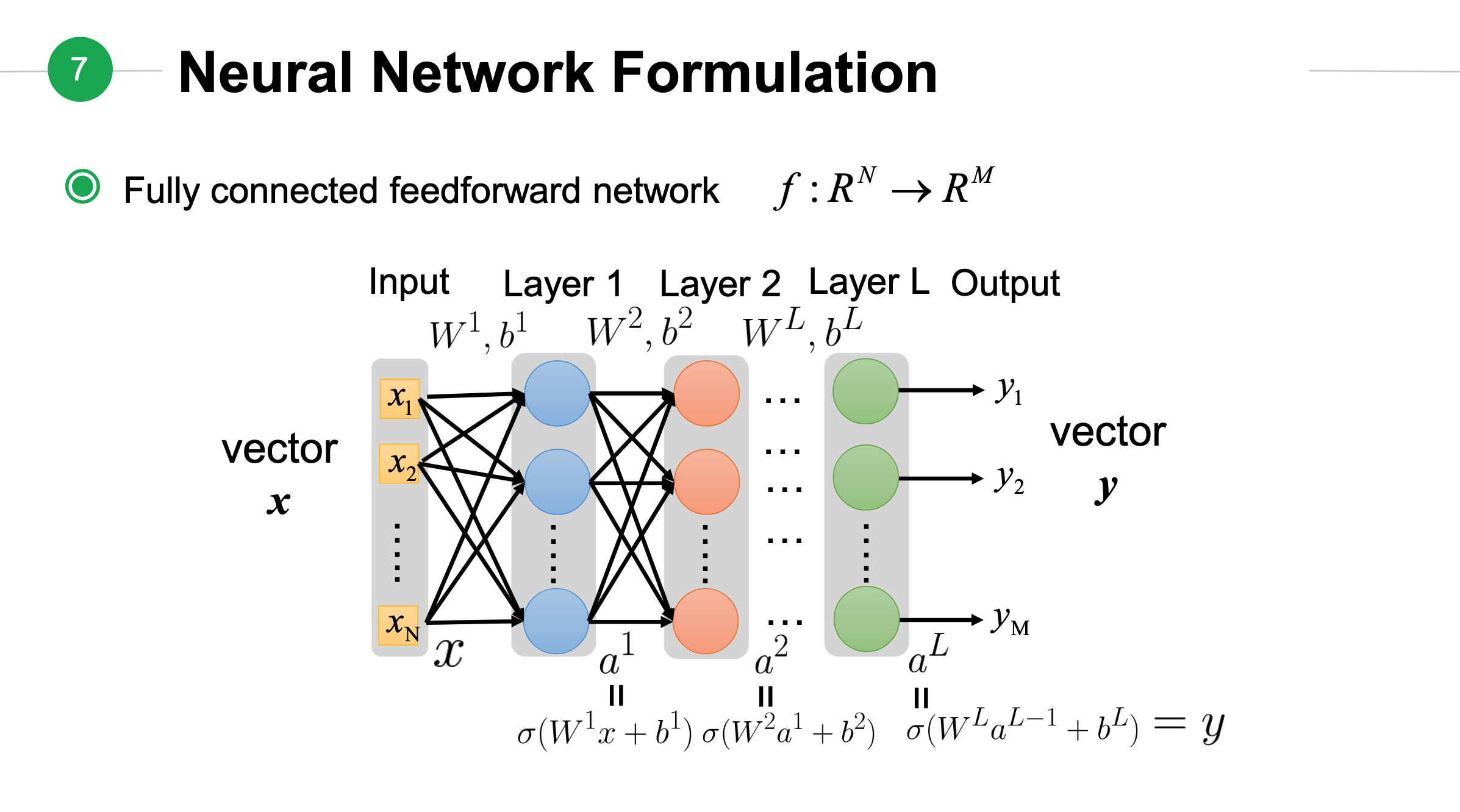
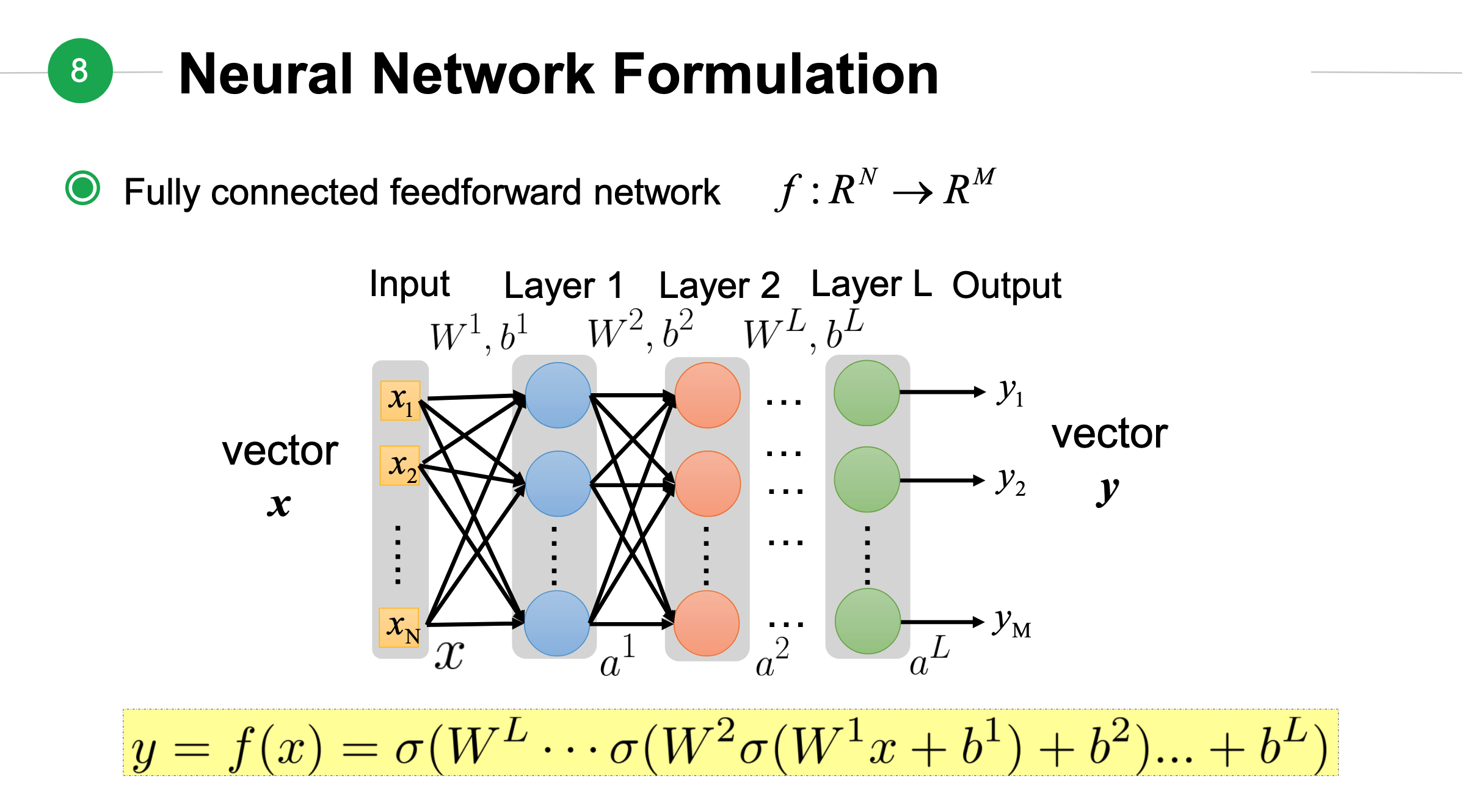
神经网络表达式

\[ \begin{aligned} & a^1 = \sigma(W^1x + b^1)\\ & a^2 = \sigma(W^2a^1 + b^2)\\ & \cdots\\ &y = a^L = \sigma(W^La^{L-1} + b^L)\\ \end{aligned} \]

从上面关系可以看出\(a^1\)可以计算出\(a^2\)，最终计算出\(a^L\).按照这个顺序依次带入公式中，我们可以得到：

\[ \mathbf{y} = f(\mathbf{x}) = \sigma(W^L\cdots\sigma(W^2\sigma(W^1\mathbf{x} + b^1) + b^2)\cdots + b^L) \]

上面公式中\(\mathbf{x}\)是输入向量，\(\mathbf{y}\)是输出向量。

损失函数

评估一个拟合函数的好坏，应该是函数预测值极大地近似真实值，即：

\[ f(x;\theta) \sim \hat{y} \]

其中： - \(\hat{y}\)是真实值，注意MSE中\(\hat{y}\)一般表示的是预测值 - \(f(x;\theta)\) 表示拟合参数为\(\theta\)时的预测函数，若是神经网络输出，表示的输入为 x、网络权重和偏置为 θ 时的预测函数。

将上面表达式转换成数学公式：

\[ \|\hat{y} - f(x;\theta)\| \approx 0 \]

从而我们可以定一个损失函数：

\[ C(\theta) = \sum_{k}\|\hat{y}_k - f(x_k;\theta)\| \]

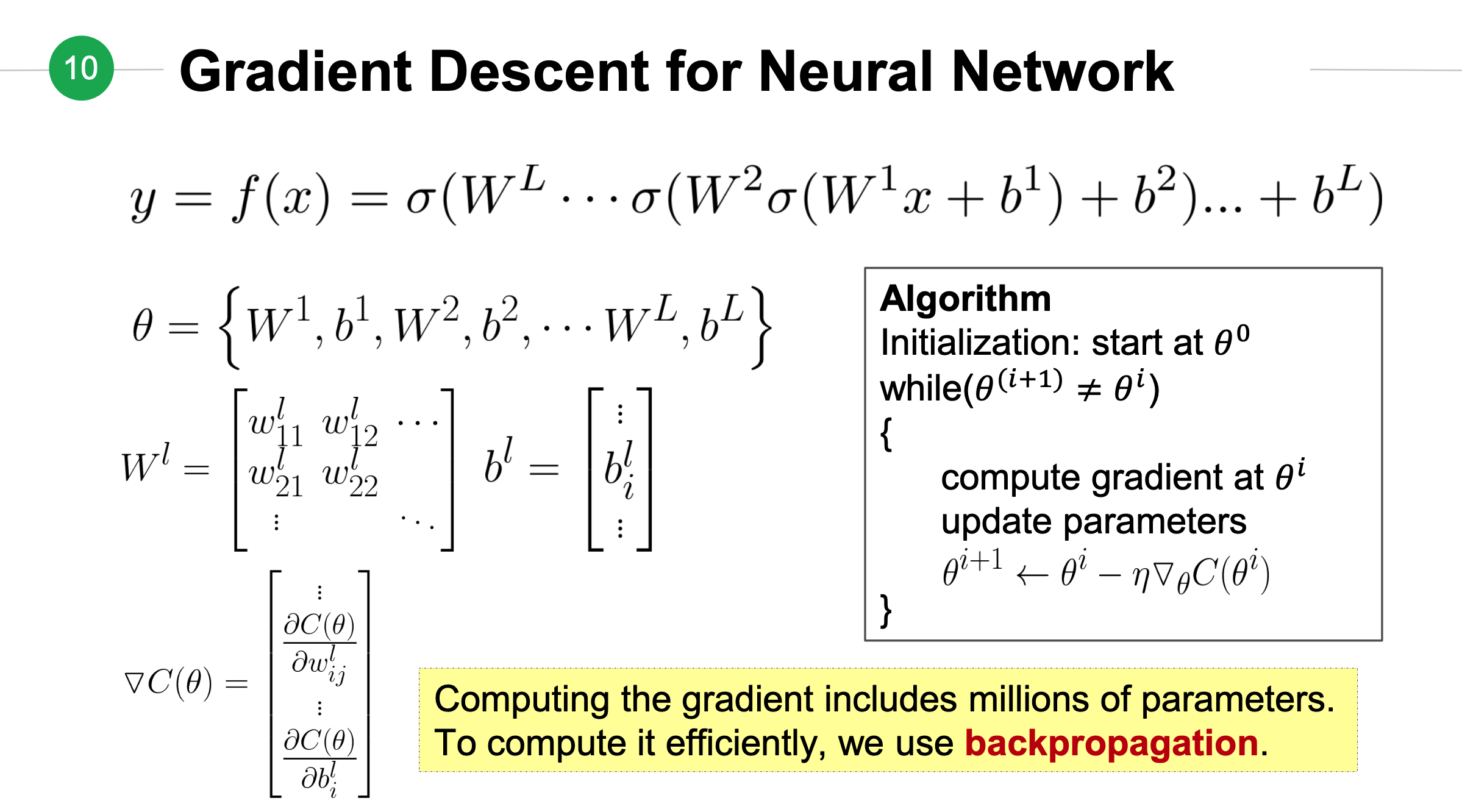
神经网络的梯度下降法

\[ \mathbf{y} = f(\mathbf{x}) = \sigma(W^L\cdots\sigma(W^2\sigma(W^1\mathbf{x} + b^1) + b^2)\cdots + b^L) \]
\[ \theta = \{W^1, b^1, W^2, b^2, \cdots,W^L, b^L\} \]
\[ W^l = \begin{bmatrix} w_{11}^l & w_{12}^l & \cdots \\ w_{21}^l & w_{22}^l & \cdots \\ \vdots & \vdots & \ddots & \\ w_{{N_l}1}^l & w_{{N_l}2}^l & \cdots \\ \end{bmatrix}\quad b^l = \begin{bmatrix} \vdots \\ b_{i}^l \\ \vdots \end{bmatrix}\quad(第i层有N_i个节点) \]
\[ \nabla C(\theta) = \begin{bmatrix} \vdots \\ \frac{\partial C(\theta)}{\partial w_{ij}^l} \\ \vdots \\ \frac{\partial C(\theta)}{\partial b_i^j} \end{bmatrix} \]

链式法则

graph LR
    w((w)) -->|f| x((x)) -->|f| y((y))-->|f| z((z))

考虑上面的神经网络网络，\(w\)神经元的微小变动\(\Delta w\)，经过激活函数\(f\)后，会影响\(x\)神经元的输入(带来了变动\(\Delta x\))，依次传递，最终影响\(z\)的结果。这个变动带来级联反应可以如下表示：

\[ \Delta w \to \Delta x \to \Delta y \to \Delta z \]

这个其实就是链式法则。我们可以\(w\)想象成带有旋钮的机器，我们调整旋钮时候可以改变\(w\)的输出，当我们扭动旋钮时候，\(w\)机器输出变化了\(\Delta w\)，依次...,具体描述参见[[链式法则#如何理解链式法则？]]

让我们来计算\(z\)关于\(w\)的偏微分，根据链式法则有：

\[ \begin{aligned} \frac{\partial z}{\partial w} &= \frac{\partial z}{\partial y}\frac{\partial y}{\partial x}\frac{\partial x}{\partial w}\\\\ &= f'(y)f'(x)f'(w)\\\\ &= f'(f(f(w)))f'(f(w))f'(w) \end{aligned} \]

当我们计算\(z\)关于\(w\)的偏微分时候，可以看到我们先计算出\(z\)关于\(y\)的偏微分，再接着计算出\(y\)关于\(x\)的偏移\(\cdots\),最后得出结果。这个计算过程跟变量输入传递过程相反，这就是反向传播（back propagation)。

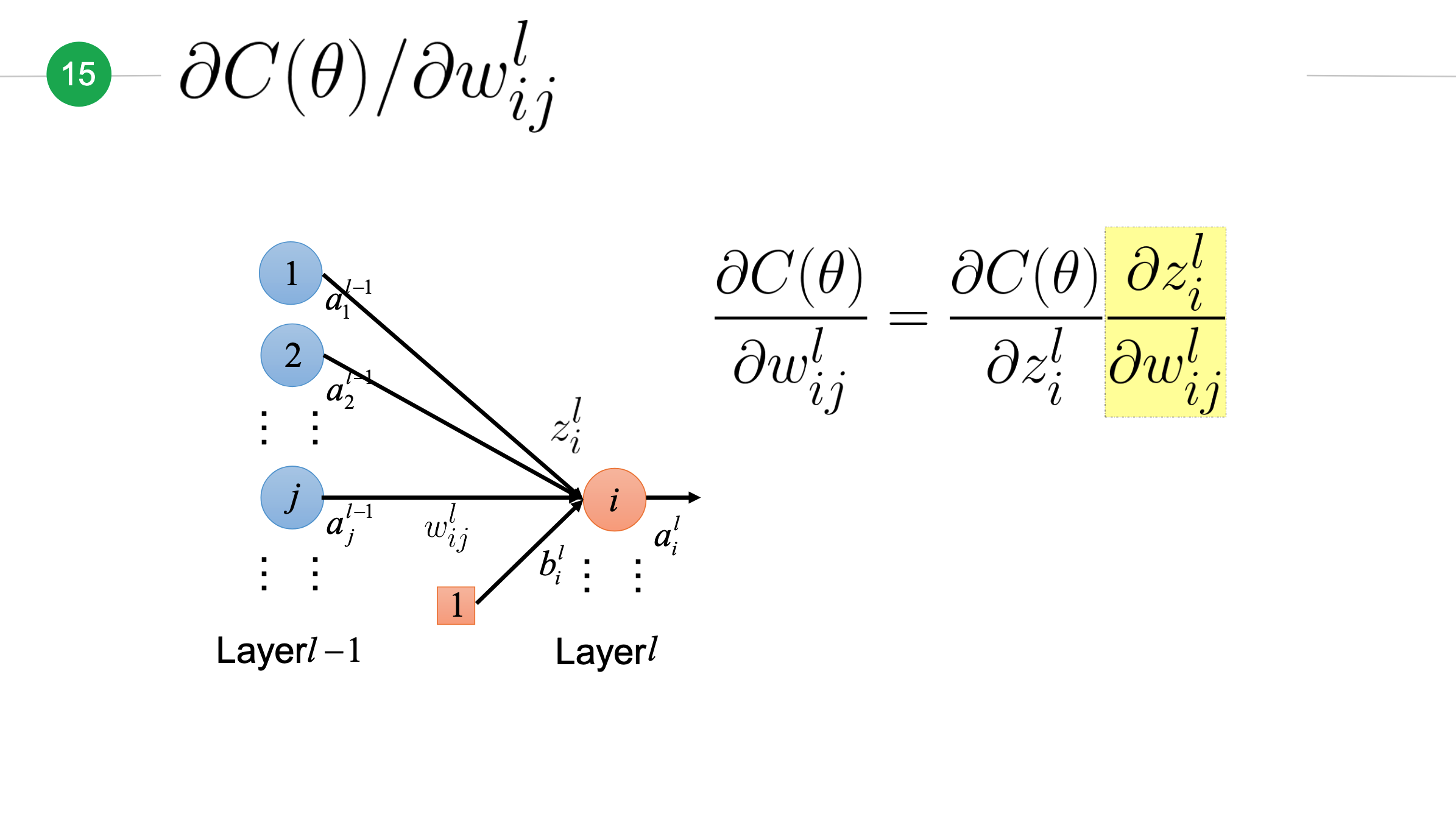
损失函数关于某个权重的偏导

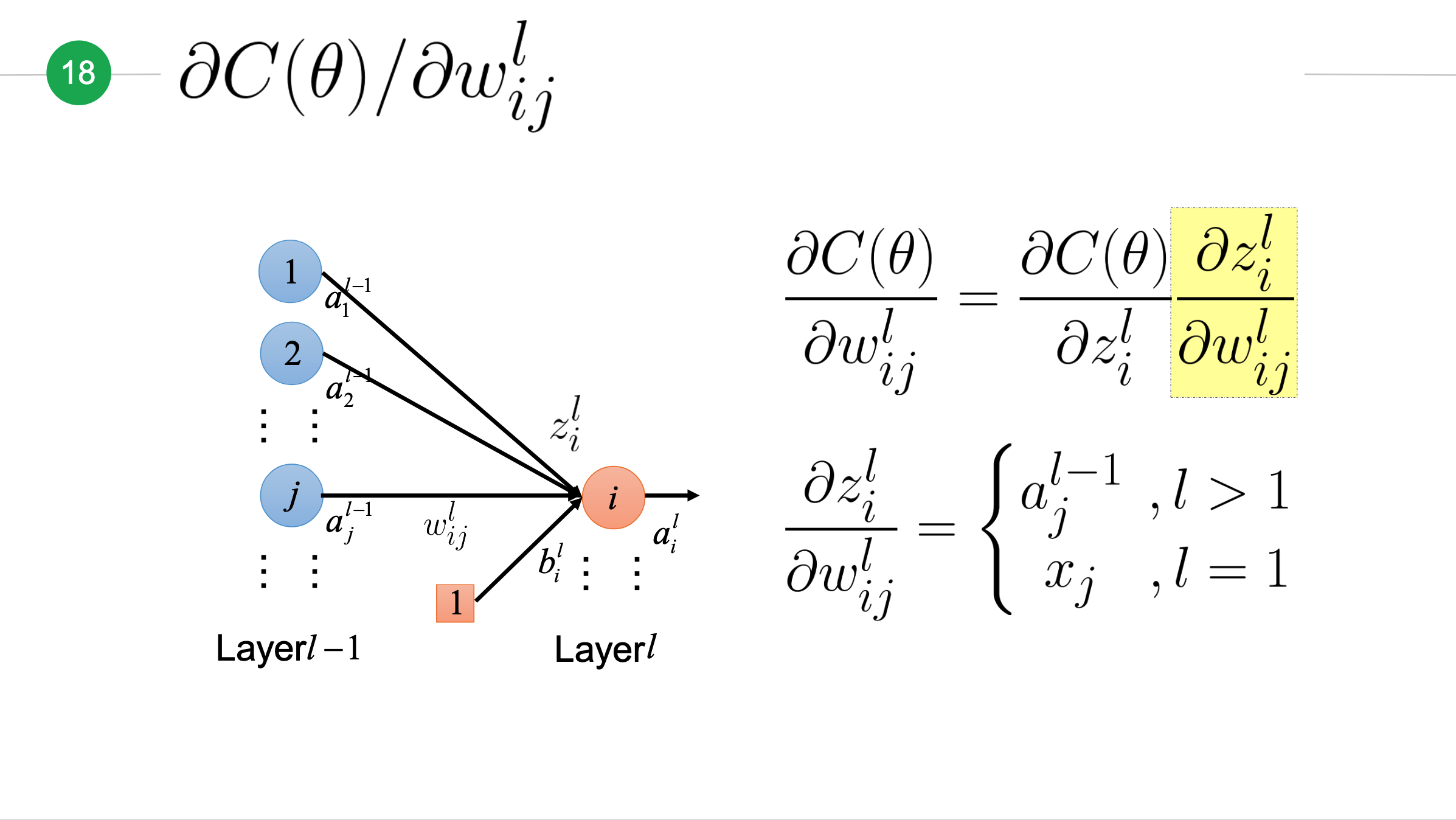
让我们来计算损失函数\(C(\theta)\)关于第\(l-1\)层第\(j\)个神经元到第\(l\)层第\(i\)个神经元的权重\(w_{ij}^l\)的偏导。由于难以直接计算出这个偏导，但考虑到\(w_{ij}^l\)变动会影响\(z_i^l\)的变动，根据上面介绍的链式法则，我们得出下面公式：

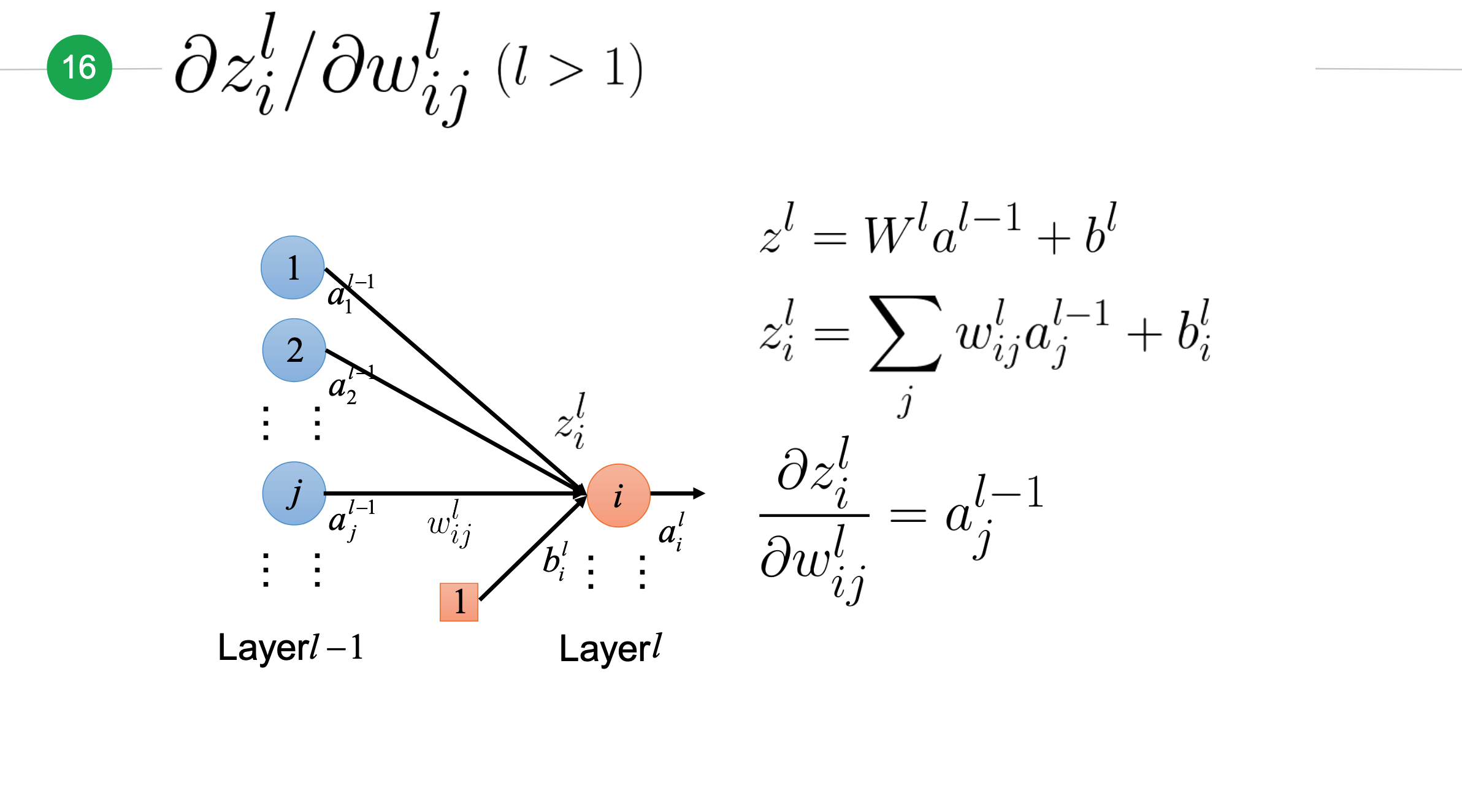
\[ \frac{\partial(\theta)}{\partial w_{ij}^l} = \frac{\partial C(\theta)}{\partial z_i^l}{\frac{\partial z_i^l}{\partial w_{ij}^l}} \]

z对w的偏微分

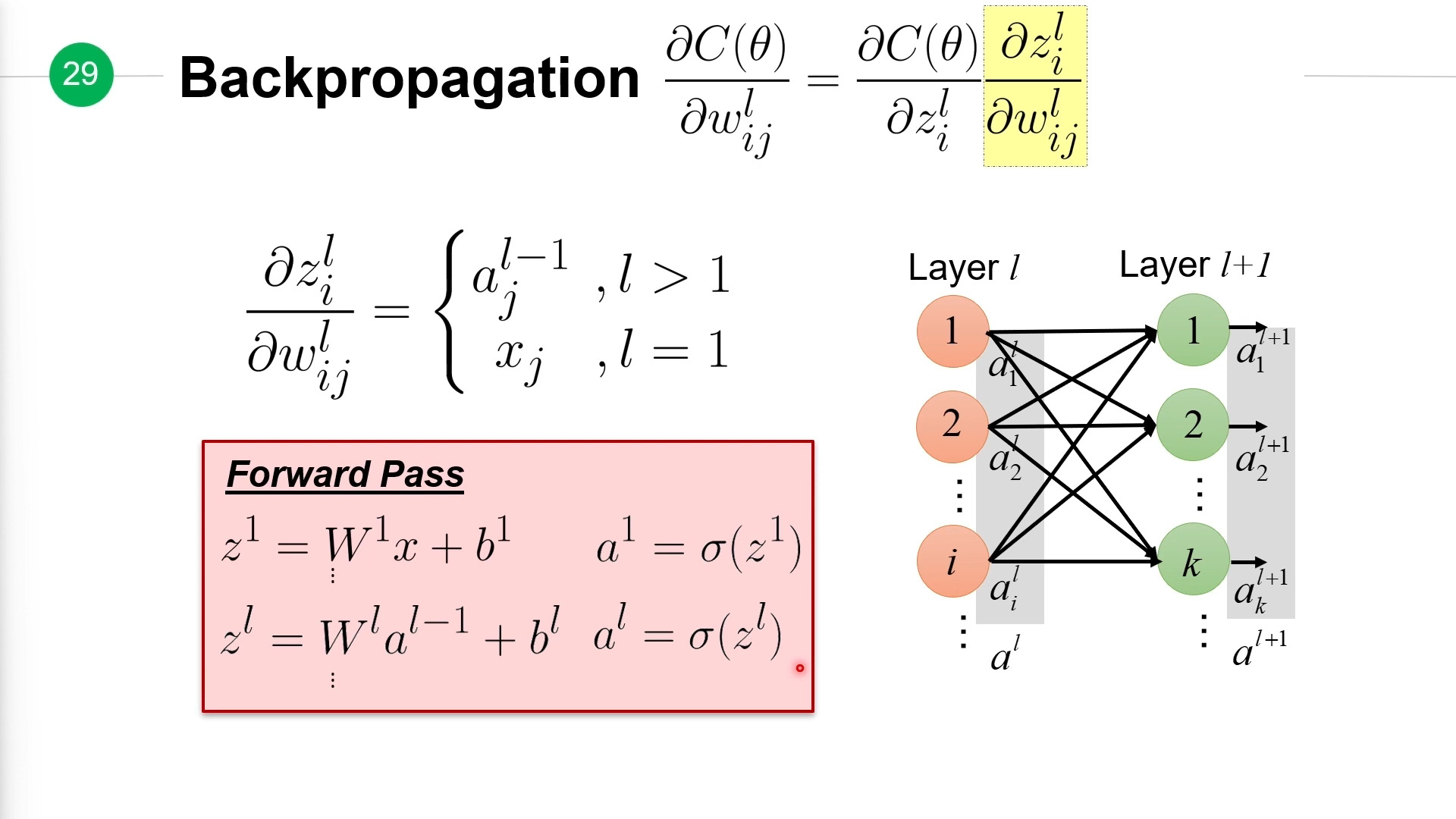
接下来我们先来计算\(z\)对\(w\)的偏微分\(\frac{\partial z_i^l}{\partial w_{ij}^l}\)，先考虑\(l>1\)（即上一层\(l-i\)不是输入层）的情况：

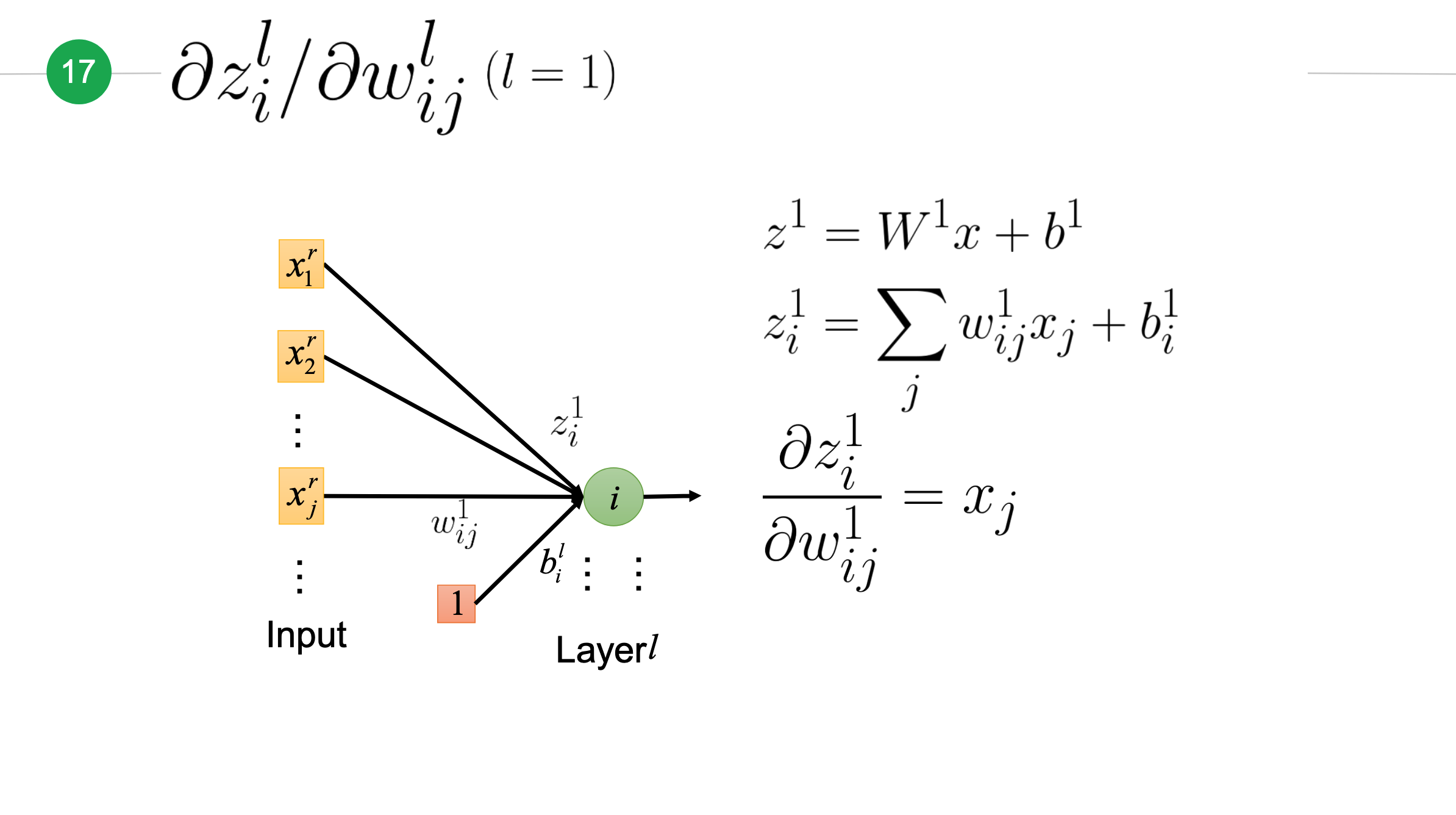
\[ \begin{aligned} &Z^l = W^lA^{l-i} + B^l \quad{（此时为向量形式，用大写符号表示更直观)}\\ &\Downarrow \\ & z_i^l = \sum_jw_{ij}^laj^{l-1} + b_i^j\\ &\Downarrow \\ &\frac{\partial z_i^l}{\partial w_{ij}^l} = a_j^{l-1} \end{aligned} \]

接下来考虑\(l=1\)时情况，此时\(l-1\)层是输入层：

那么最终\(z\)对\(w\)的偏微分：

\[ \frac{\partial z_i^l}{\partial w_{ij}^l} = \begin{cases} a_j^{l-1}, \quad l > 1 \\ x_j, \quad l = 1 \end{cases} \]
计算误差项\(\delta i\)
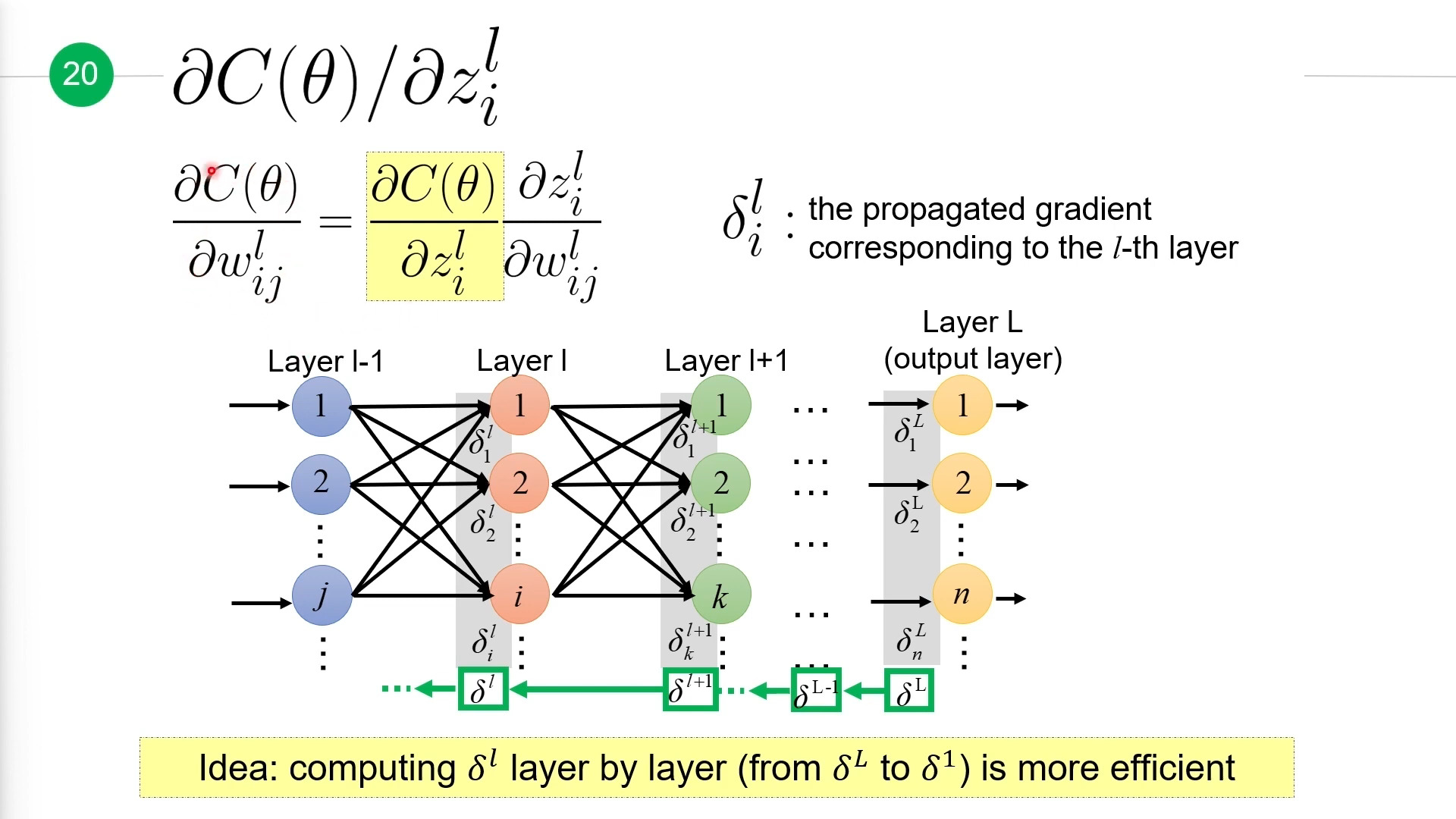
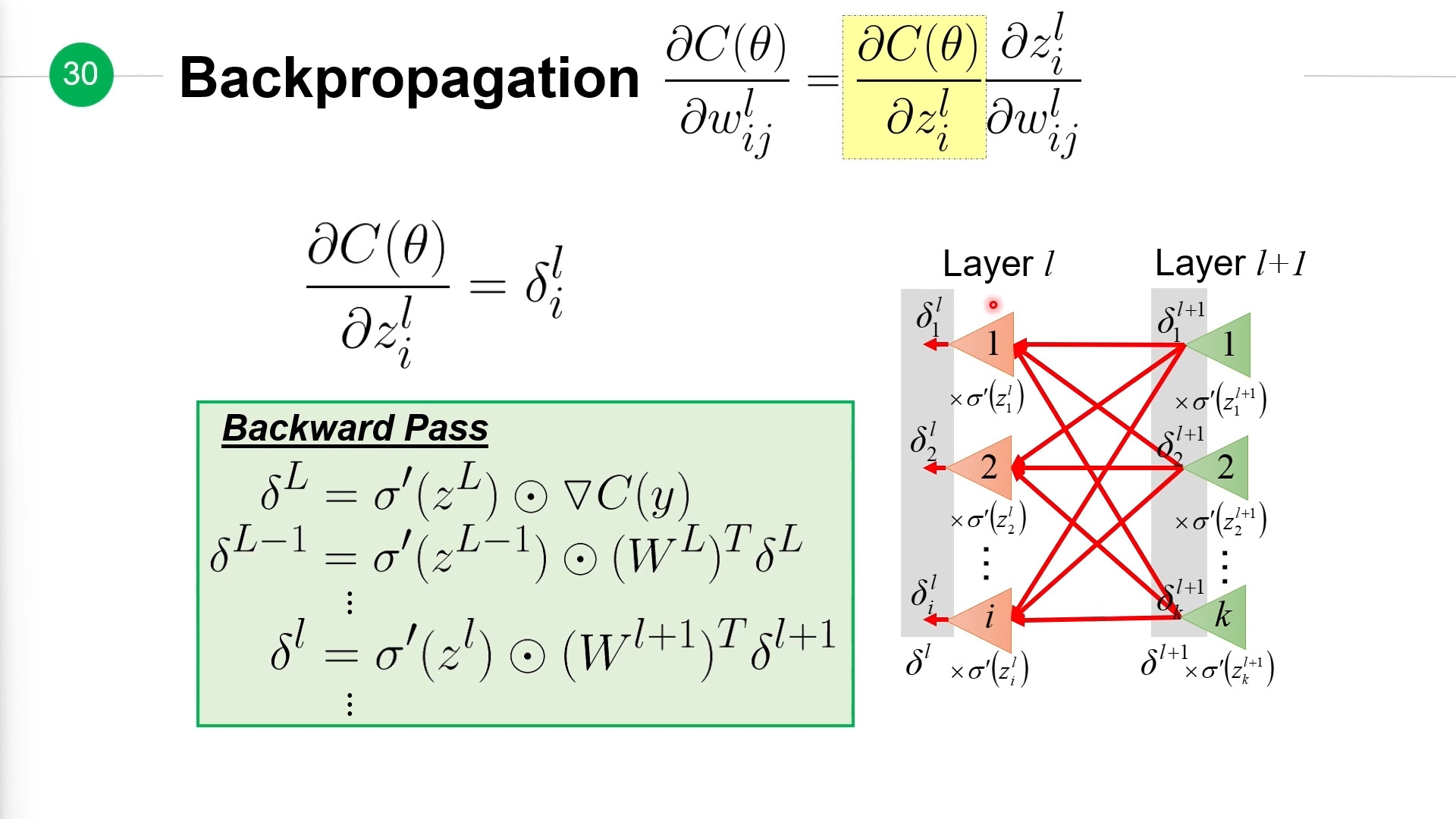
\[ \frac{\partial(\theta)}{\partial w_{ij}^l} = \boxed{\frac{\partial C(\theta)}{\partial z_i^l}}{\frac{\partial z_i^l}{\partial w_{ij}^l}} \]

接下来我们计算剩余的\(\frac{\partial C(\theta)}{\partial z_i^l}\),这里我们引入符号\(\delta i^l\)来表示这个偏微分，也就是说它表示的是损失函数\(C(\theta)\)对第\(l\)层第\(i\)层神经元的加权输入\(z_i^l\)的偏微分,也叫做误差项。

\[ \delta i^l = \frac{\partial C(\theta)}{\partial z_i^l} \]

计算\(\delta ^l\)(\(\delta ^l\)是第\(l\)所有误差项组成的向量，包含\(\delta_i^l\))时，我们可以从\(\delta^L\)到\(\delta^l\),一层一层的反方向计算出来,这样计算更高效。

计算思路：

  1. 先计算\(\delta^L\)。

计算\(\delta^L\)：

由于：

\[ \delta_i^L = \frac{\partial C}{\partial z_i^L}\quad \quad \Delta z_i^L \to \Delta a_i^L = \Delta y_i \to \Delta C \]

所以：

\[ \begin{aligned} &\delta_i^L = \frac{\partial C}{\partial z_i^L} \\ &= \frac{\partial C}{\partial y_i}\frac{\partial y_i}{\partial z_i^l} \quad{(依据上面的链式法则)}\\ &= \boxed{\frac{\partial C}{\partial y_i}}\frac{\partial y_i}{\partial z_i^l} \quad{(圈中部分依赖损失函数定义)}\\ &= \frac{\partial C}{\partial y_i}\frac{\partial \boxed{y_i = a_i^L = \sigma(z_i^L)}} {\partial z_i^l}\\ &= \frac{\partial C}{\partial y_i}\sigma'(z_i^L)\\ &=\Delta C(y)\sigma'(z_i^L) \end{aligned} \]

上面是单个误差项，整个\(L\)的误差项是：

\[ \delta ^L = \sigma'(z^L)\odot \nabla C(y) \]

现在基于\(\delta^{l+1}\)来计算\(\delta ^l\):

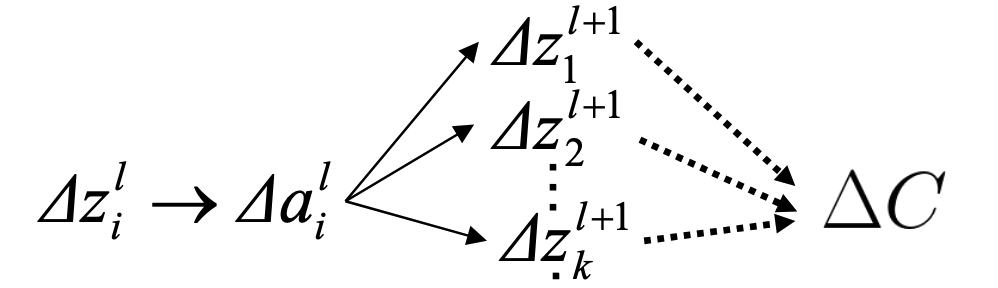
考虑到\(z_i^l\)的微小变化会影响\(a_i^l\)，而\(a_i^l\)会影响第\(l+1\)层的\(z\),进而影响\(l+1\)的\(a\)，进而影响第\(l+2\)层，依次下去最终影响到\(C\)。依赖传递关系如下：

\[ \Delta z_i^l \to \Delta a_i^l \to Z^{l+1} \to A^{l+1} \to \cdots \to \Delta C\quad{(Z、A是向量)} \]

\[ \begin{aligned} \delta i^l &= \frac{\partial C(\theta)}{\partial z_i^l} \\ &=\sum_k(\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial a_i^l}\frac{\partial a_i^l}{\partial z_i^l})\\ &= \frac{\partial a_i^l}{\partial z_i^l}\sum_k (\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial a_i^l}) \quad{(提取出与k无关的公共部分)}\\ &= \frac{\partial a_i^l}{\partial z_i^l}\sum_k (\boxed{\frac{\partial C}{\partial z_k^{l+1}}}\frac{\partial z_k^{l+1}}{\partial a_i^l}) \quad{(\frac{\partial C}{\partial z_k^{l+1}} 即为\delta_k^{l+1})}\\ &= \frac{\partial a_i^l}{\partial z_i^l}\sum_k (\frac{\partial z_k^{l+1}}{\partial a_i^l}\delta_k^{l+1}) \\ &= \boxed{\frac{\partial a_i^l}{\partial z_i^l} = \frac{\partial \sigma(z_i^l)}{\partial z_i^l}}\sum_k (\frac{\partial z_k^{l+1}}{\partial a_i^l}\delta_k^{l+1}) \\ &= \sigma'(z_i)\sum_k (\frac{\partial z_k^{l+1}}{\partial a_i^l}\delta_k^{l+1}) \\ &= \sigma'(z_i)\sum_k (\frac{\partial \boxed{z_k^{l+1} = \sum_i{w_{ki}^{l+1}a_i^l + b_k^{l+1}}}}{\partial a_i^l}\delta_k^{l+1}) \\ &= \sigma'(z_i)\sum_k (\frac{\partial \boxed{z_k^{l+1} = \sum_i{w_{ki}^{l+1}a_i^l + b_k^{l+1}}}}{\partial a_i^l}\delta_k^{l+1}) \\ &= \sigma'(z_i)\sum_k (w_{ki}^{l+1}\delta_k^{l+1}) \end{aligned} \]

最终我们得到：

\[ \delta_i^l = \sigma'(z_i)\sum_k (w_{ki}^{l+1}\delta_k^{l+1}) \]

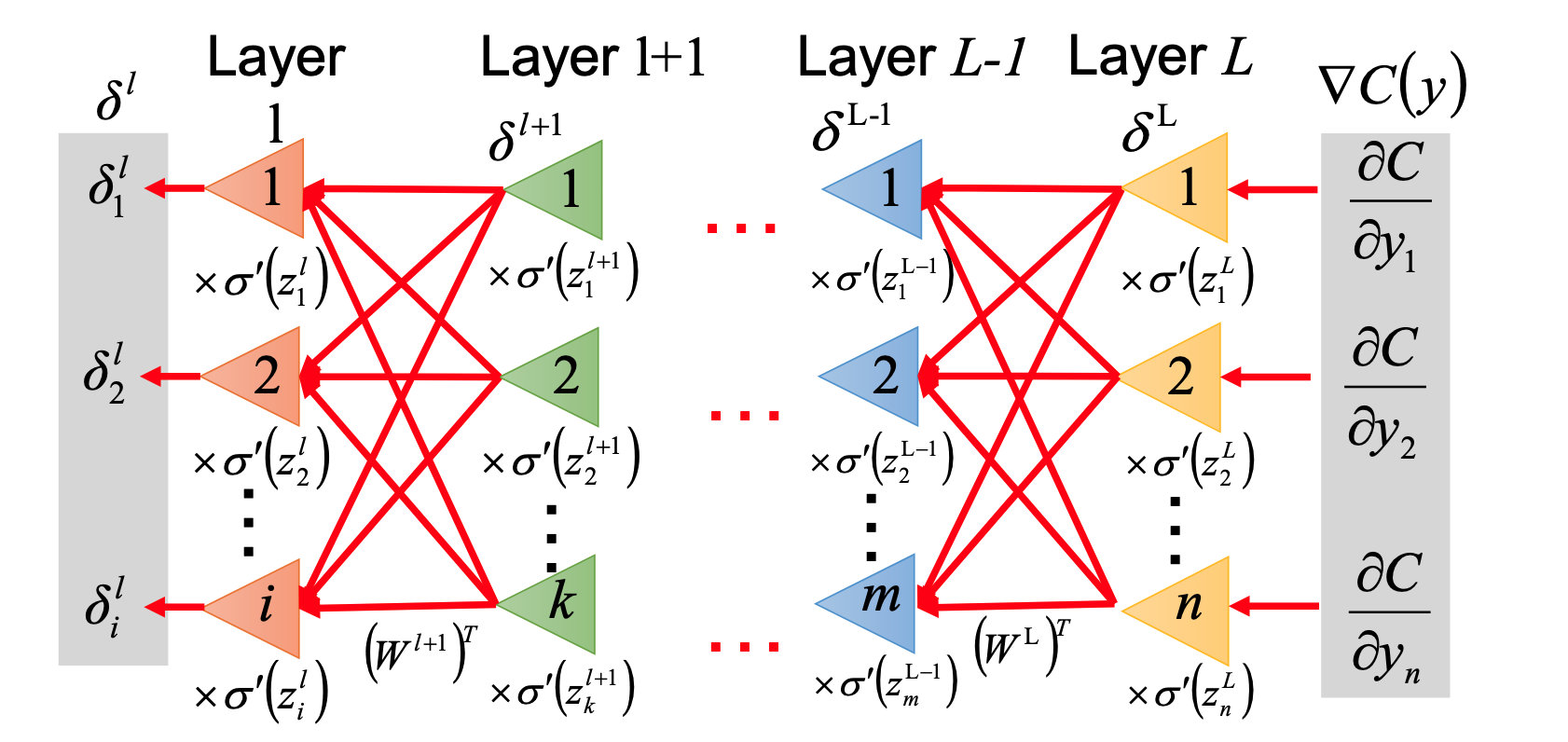
从上面式子中，我们可以发现\(\delta_i^l\)相当于第\(l+1\)层的\(\delta\)分别乘以对应边上的权重后计算出它们的和，再乘以\(\sigma'(z_i)\)，这么一个反向过程得到。如下图所示：

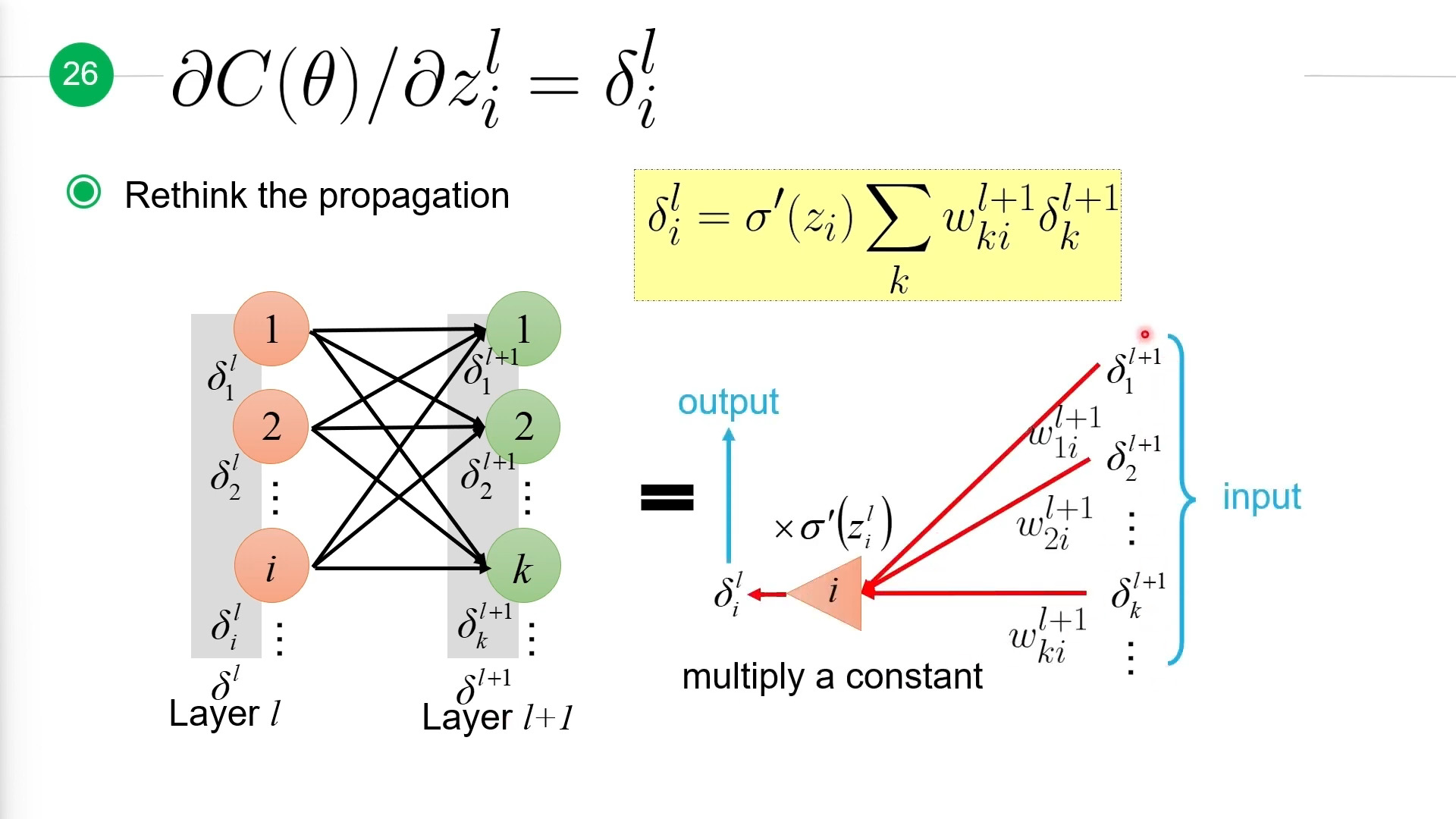
对于第\(l\)层整一层的\(\Delta^l\),计算方式如下：

\[ \begin{aligned} &\delta_i^l = \sigma'(z_i)\sum_k (w_{ki}^{l+1}\delta_k^{l+1}) \\ &\sigma'(z^l) = \begin{bmatrix} \sigma'(z_1^l) \\ \sigma'(z_2^l) \\ \vdots \\ \sigma'(z_i^l) \\ \vdots \end{bmatrix}\\ &\delta^l = \sigma'(z^l) \odot (W^{l+1})^T\delta^{l+1} \end{aligned} \]

结合上面计算得到的\(\delta^L\)，以及\(\delta^l\)公式，我们就可以反向计算出所有层的\(\delta\):

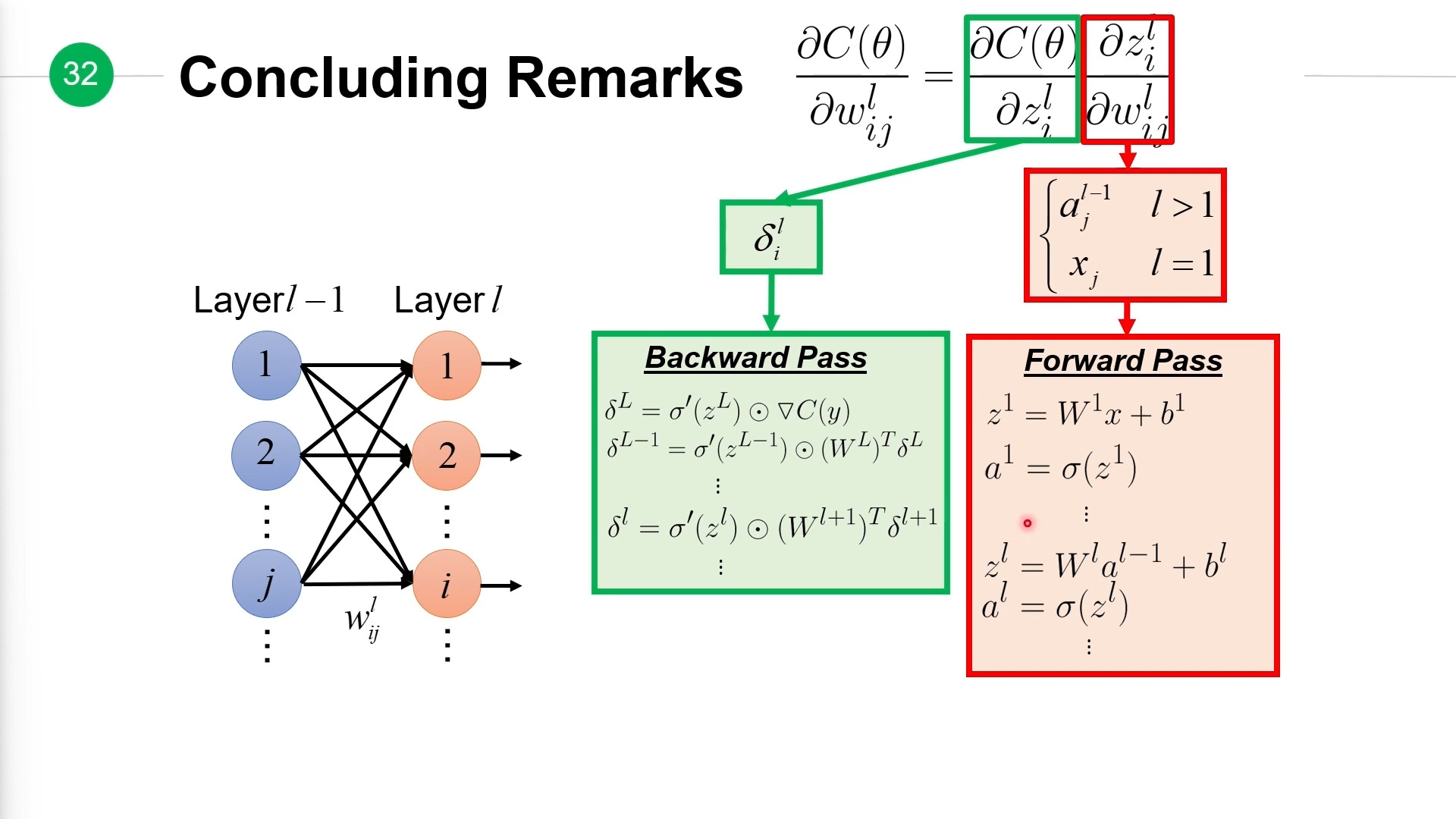
\[ \begin{aligned} &\delta^L = \sigma'(z^L) \odot \nabla C(y)\\\\ &\delta^l = \sigma'(z^l) \odot (W^{l+1})^T\delta^{l+1}\\ \end{aligned} \]

完整过程

计算损失函数关于权重的偏导\(\frac{\partial C(\theta)}{\partial w_{ij}^l}\)，分两步走。

第一步正向传播(Forward Pass)计算出所有\(z\)、\(a\)值：

第二步反向传播，根据第一步计算出来的值，计算出所有误差：

最后一步：

根据这个过程计算出所有的权重值的偏导，然后利用梯度下降法可以不停的更新整个权重。

评论