深度学习的数学

chap2 神经网络的数学基础

函数

定义

有两个变量\(x\)和\(y\)，如果对每个\(x\)都有唯一确定的\(y\)与它对应，则称\(y\)是\(x\)的函数，用\(y=f(x)\)表示，此时称\(x\)为自变量，\(y\)为因变量。

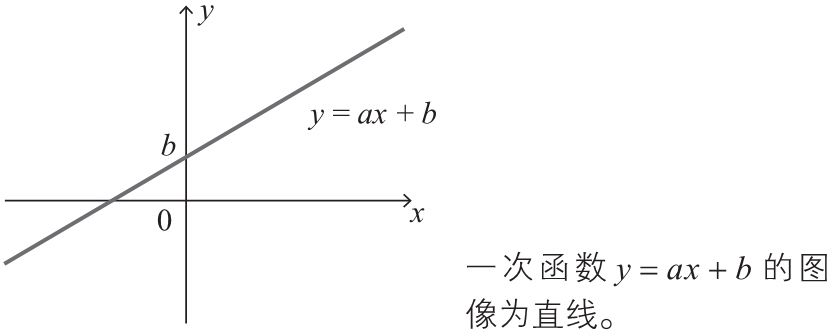
一次函数

\[ y = ax + b \quad \text{(a、b为常数，}a\ne 0\text{)}\quad \quad(1) \]

当两个变量\(x\)、\(y\)满足式(1)的关系时候，称变量\(y\)和变量\(x\)是一次函数关系。

上面式子中\(a\)称为斜率，\(b\)称为截距。上面式子的函数图像如下：

对于多个自变量，比如，有两个变量\(x_1\),\(x_2\),当它们满足下式的关系时，称\(y\)和\(x_1\)、\(x_2\)是一次函数关系：

\[ y = ax_1 + bx_2 + c \quad{(a、b、c为常数，a\ne 0, b\ne 0)} \]

神经单元的加权输入与一次函数

在神经网络中，神经单元的加权输入可以表示为一次函数关系。比如下面是神经单元有三个来自上一层的输入，其加权输入\(z\)的表达式：

\[ z = w_1x_1 + w_2x_2 + w_3x_3 + b \]

如果把作为参数的权重\(w_1\)、\(w_2\)、\(w_3\)与偏置\(b\)看作常数，那么加权输入\(z\)和\(x_1\)、\(x_2\)、\(x_3\)是一次函数关系。另外，在神经单元的输入\(x_1\)、\(x_2\)、\(x_3\)作为数据值确定了情况下，加权输入\(z\)和权重\(w_1\)、\(w_2\)、\(w_3\)以及偏置\(b\)是一次函数关系。

二次函数

二次函数由下式表示：

\[ y = ax^2 + bx + c \quad{(a、b、c为常数，a\ne 0)} \]

单位阶跃函数

神经网络的原型函数是用单位阶跃函数作为激活函数的。它的图像和式子如下；

\[ u(x) =\left \{ \begin{array}{l} % l 靠左、c 居中、r 靠右 0 ( x\gt 0)\\\\ 1 (x \ge 0) \end{array} \right. \]

由于单位阶跃函数在原点处不可导，它不能成为主要的激活函数。

指数函数

具有以下形状的函数称为指数函数：

\[ y = a^x\quad{(a为正的常数，a\ne 1)} \]

常数\(a\)称为指数函数的底数。纳皮尔数\(e\)是一个特别重要的底数，其近似值如下：

\[ e = 2.71828\cdots \]

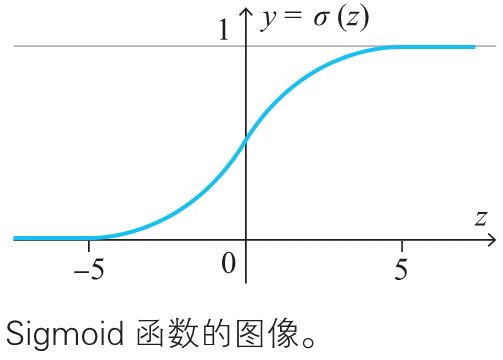
Sigmoid函数

Sigmoid函数是神经网络中具有代表性的激活函数。

\[ \sigma(x) = \frac{1}{1+e^{-x}} = \frac{1}{1 + exp(-x)} \]

上面公式中exp是exponential function(指数函数)的简略记法，\(exp(x)\)表示指数函数\(e^x\)。

数列

定义

数列是数的序列。数列中的每一个数称为项。排在第一位的项称为首项，排在第二位的项称为第\(2\)项，排在第\(3\)的项称为第三项，以此类推，排在第\(n\)位的项称为第\(n\)项。

具有有限项的数列称为有穷数列，在有穷数列中，数列的最后一项称为末项。

数列的通项公式

数列中排在第\(n\)位的数，通常用\(a_n\)表示，整个数列可以用符号\(\{a_n\}\)来表示。

将数列的第\(n\)项用一个关于\(n\)的式子表示出来，这个式子就称为该数列的通项公式。

数列与递推关系式

除了通项公式，数列还可以使用相邻项的关系式来表示，这种表示法称为数列的递归定义。

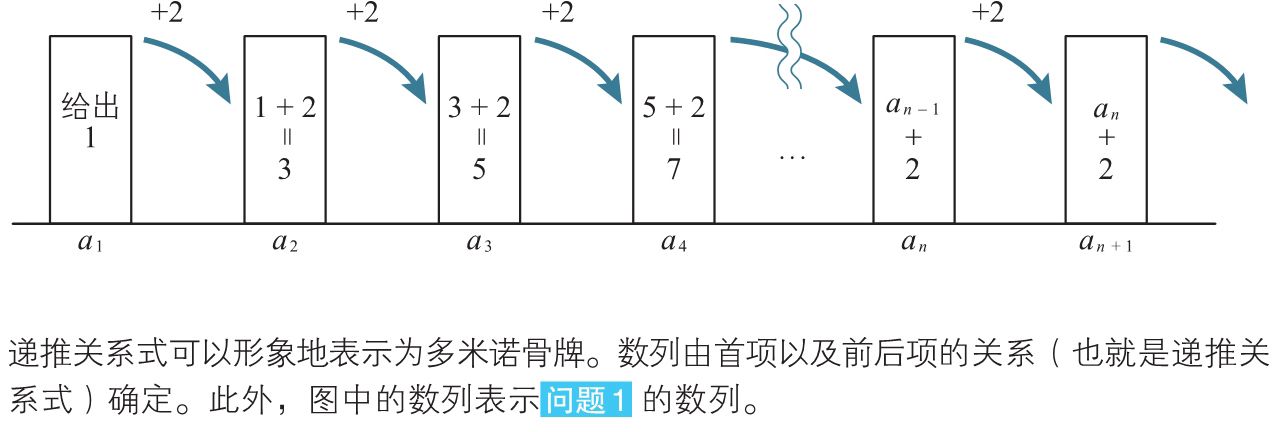
一般地，如果已知首项\(a_1\)以及相邻两项\(a_n\)、\(a_{n+1}\)的关系式，就可以确定这个数列，这个关系式称为递推关系式。

已知首项\(a_1 = 1\)，以及关系式\(a_{n+1} = a_n + 2\),可以确定一下数列，这个关系式就是数列的递推关系式。

\[ \begin{aligned} a_1 &= 1\\ a_2 &= a_{1+1} = a_1 + 2 = 1+2 = 3\\ a_3 &= a_{2+1} = a_2 + 2 = 3 + 2 = 5\\ a_4 &= a_{3+1} = a_3 + 2 = 5 + 2 = 7\\ \cdots \end{aligned} \]

联立递推关系式

将多个数列的递推关系式联合起来组成一组，称为联立递推关系式。在神经网络的世界中，所以神经单元的输入和输出在数学上都可以认为是用联立递推式联系起来的。

Σ符号

\(\sum\) 符号用于表示数列的总和。

[!warning] 注意 \(\sum\)为希腊字母，对应拉丁字母\(S\)，即Sum的首字母。 在希腊本土或纯希腊字母表中，\(\sum\) 和 \(\sigma\) 两者均读 "sigma"。但数学语境下通常把求和符号 ∑ 读作 "sigma（求和）"，而 σ 读作 "sigma（变量）"。

对于数列\({a_n}\)，\(\sum\)符号的定义式如下所示：

\[ \sum_{k=1}^{n}a_k = a_1 + a_2 + a_3 + ... + a_{n-1} + a_n \]

上面式子中，字母\(k\)并不具有实质的含义，\(k\)仅用于表明关于它求和，这个字母并非必须\(k\)，在数学上通常使用\(i\)、\(j\)、\(k\)、\(l\)、\(m\)、\(n\)。

Σ符号的性质

\(\sum\)符号具有线性性质。与导数公式“和导数为导数的和”，“常数倍的导数为导数的常数倍”类似，“和的\(\sum\)为\(\sum\)的和”，“常数倍的\(\sum\)为\(\sum\)的常数倍。

\[ \sum_{k=1}^n(a_k + b_k) = \sum_{k=1}^na_k + \sum_{k=1}^nb_k \quad(1) \]

\[ \sum_{k=1}^nca_k = c\sum_{k=1}^na_k\quad{（c为常数）} \]

证明

根据\(\sum\)符号的定义，有：

\[ \begin{aligned} \sum_{k=1}^n(a_k + b_k) &= (a_1 + b_1) +(a_2 + b_2) + \cdots + (a_n + b_n)\\ &= (a_1 + a_2 + \cdots + a_n) + (b_1 + b_2 + \cdots + b_n)\\ &= \sum_{k=1}^na_k + \sum_{k=1}^nb_k \end{aligned} \]

\[ \begin{aligned} \sum_{k=1}^nca_k &= ca_1 + ca_2 + \cdots + ca_n \\ &= c(a_1 + a_2 + \cdots + a_n)\\ &= c\sum_{k=1}^na_k \end{aligned} \]

向量

有向线段与向量

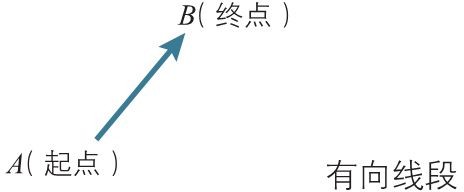
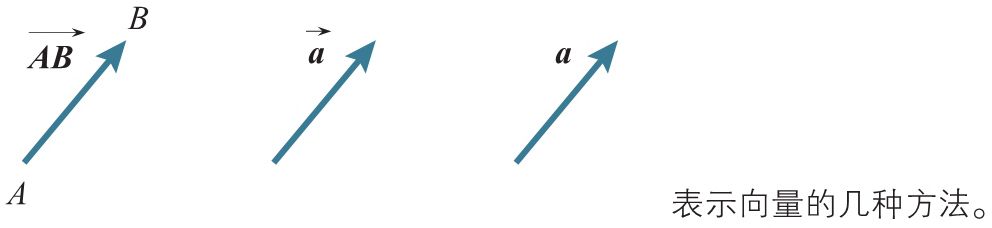
有两个点\(A\)、\(B\)，我们考虑从\(A\)指向\(B\)的线段，这条具有方向的线段\(AB\)叫做有向线段，其中\(A\)为起点，\(B\)为终点。

有向线段\(AB\)具有以下属性：起点\(A\)的位置，指向\(B\)的方向，以及\(AB\)的长度（即大小）。在三个属性中，把方向和大小抽象出来，这样的量叫做向量。

向量是具有方向和大小的量

有向线段\(AB\)所大表的向量用\(\overrightarrow{AB}\)表示，也可以用带箭头的单个字母\(\mathbf{\overrightarrow{a}}\)或者不带箭头的黑斜体字母\(\mathbf{a}\)表示。

向量的坐标表示

把箭头的起点放在原点，用箭头终点的坐标表示向量，这叫做向量的坐标表示。

向量的大小

从直观上来讲，表示向量的箭头的长度称为这个向量的大小。向量\(\mathbf{a}\)的大小用\(|\mathbf{a}|\)表示。

向量的内积

两个向量\(\mathbf{a}\)、\(\mathbf{b}\)的内积\(\mathbf{a}\cdot\mathbf{b}\)的定义如下：

\[ \mathbf{a}\cdot\mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta\quad{（\theta为\mathbf{a},\mathbf{b}的夹角）} \]

柯西-施瓦茨不等式

\[ -|\mathbf{a}||\mathbf{b}| \le \mathbf{a}\cdot \mathbf{b} \le |\mathbf{a}||\mathbf{b}| \]

证明如下：

根据余弦函数的性质，对任意的\(\theta\) ,有\(-1 \le \cos\theta \le 1\),两边同时乘以\(|\mathbf{a}||\mathbf{b}|\)，有：

\[ -|\mathbf{a}||\mathbf{b}| \le \mathbf{a}\cdot \mathbf{b} \le |\mathbf{a}||\mathbf{b}| \]

当两个向量\(\mathbf{a}\)、\(\mathbf{b}\)的大小固定时，根据柯西-施瓦茨不等式，可以得出以下事实： - 当两个向量方向相反时候，内积取得最小值。 - 当两个向量不平行时，内积取值取平行时的中间值。 - 当两个向量方法相同时候，内积取得最大值。

内积的坐标表示

在平面中向量内积可以表示如下：

当\(\mathbf{a} = (a_1, a_2), \mathbf{b} = (b_1,b_2)\)时，\(\mathbf{a}\cdot\mathbf{b} = a_1b_1 + a_2b_2\)

在三维空间中，内积的坐标表示如下所示：

当\(\mathbf{a} = (a_1,a_2, a_3)\),\(\mathbf{b} = (b_1,b_2,b_3)\)时，\(\mathbf{a}\cdot\mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3\)。

推广到任意的\(n\)维空间，有：

对于两个向量\(\mathbf{a} = (a_1, a_2, \cdot, a_n)\),\(\mathbf{b} = (b_1,b_2,\cdot,b_n)\),其内积\(\mathbf{a}\cdot\mathbf{b}\)如下式所示：

\[ \mathbf{a}\cdot\mathbf{a} = a_1b_1 + a_2b_2 + \cdot + a_nb_n \]

矩阵

矩阵是数的阵列。

\[ A = \left ( \begin{matrix} 3 & 1 & 4\\ 1 & 5 & 9 \\ 2 & 6 & 5 \\ \end{matrix} \right ) \]

在上式中A是3行3列构成的矩阵。若行数与列数相同的矩阵称为方阵。

如下所示的矩阵\(X\)、\(Y\)分别称为列向量、行向量，也可简称为向量。

\[ X = \left ( \begin{matrix} 3 \\ 1 \\ 4 \end{matrix} \right ), Y = \left ( \begin{matrix} 2 & 7 & 1 \end{matrix} \right ) \]

我们将矩阵\(A\)推广到更一般的情形，如下所示：

\[ \begin{split}\mathbf{A}=\left (\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{matrix}\right )\end{split} \]

上面是一个\(m\)行\(n\)列的矩阵。位于第\(i\)行第\(j\)列的值（称为元素）用\(a_{ij}\)表示。

单位矩阵

若一个方阵，它对角线上的元素\(a_{ii}\)为1，其他元素为0，我们称为单位矩阵，通常用\(E\)表示。

[!note] 笔记 \(E\)为德语中表示为1的单词Ein的首字母

矩阵相等

两个矩阵\(A\)、\(B\)相等的含义是它们对应的元素相等，记为\(A=B\)。

矩阵的和、差、常数倍

两个矩阵\(A\)、\(B\)的和\(A+B\)、差\(A-B\)定义为相同位置的元素的和、差所产生的矩阵。矩阵的常数倍定义为各个元素常数倍所产生的矩阵。

矩阵的乘积

对于两个矩阵\(A\)、\(B\),将\(A\)的第\(i\)行看做行向量，B的\(j\)列看做列向量，将它们的内积作为第\(i\)行第\(j\)列元素，由此产生的矩阵就是矩阵\(A\)、\(B\)的乘积\(AB\)。

单位矩阵\(E\)与任意矩阵\(A\)的乘积都满足交换律，即；

\[ AE = EA = A \]

而其他矩阵间的乘法不满足交换律，即：

\[ AB \ne BA \]

Hadamard乘积

对于相同形状的矩阵\(A\)、\(B\)，将相同位置的元素相乘，由此产生的矩阵称为矩阵\(A\)、\(B\)的 Hadamard 乘积，用\(A \odot B\)表示。

例如，当\(A = \left ( \begin{matrix} 2 & 7\\ 1 & 8 \end{matrix} \right )\), \(B = \left ( \begin{matrix} 2 & 8\\ 1 & 3 \end{matrix} \right )\)时：

\[ A\odot B = \left ( \begin{matrix} 2\cdot 2 & 7 \cdot 8\\ 1 \cdot 1 & 8 \cdot 3 \end{matrix} \right ) = \left ( \begin{matrix} 4 & 56\\ 1 & 24 \end{matrix} \right ) \]

转置矩阵

将矩阵\(A\)的第\(i\)行第\(j\)列的元素与第\(j\)行第\(i\)列的元素交换，由此产生的矩阵称为矩阵\(A\)的转置矩阵（transposed matrix)，记作\(A^T\)。

导数

定义

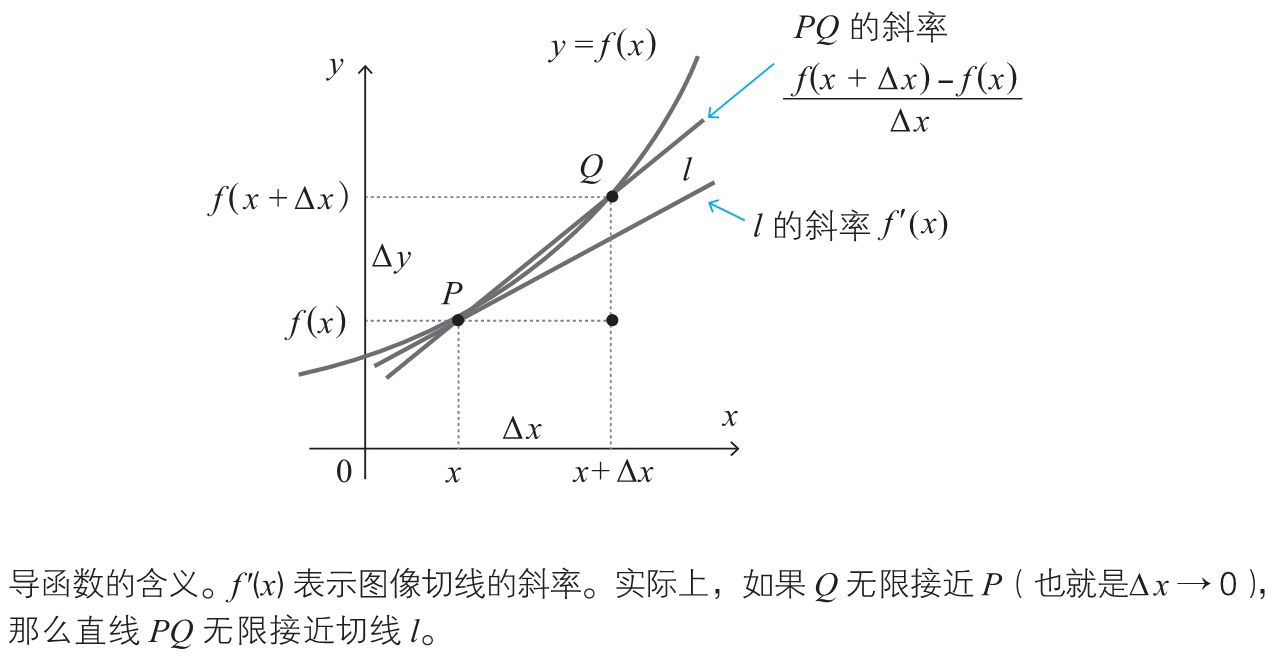
函数\(y=f(x)\)导函数\(f'(x)\)的定义如下所示：

\[ f'(x) = \lim_{\Delta x \to 0}\frac{f(x + \Delta x) - f(x)}{\Delta x} \quad{(1)} \]

上面式子中希腊字母\(Delta\)读作\(delta\)，对应拉丁字母\(D\)，此外，带有\('\)(prime)符号的函数或者变量表示导函数。

已知函数\(f(x)\)，求导函数\(f'(x)\)，称为对函数\(f(x)\)求导，当式(1)的值存在时，称函数可导。

导函数的几何含义下图所示：

函数\(y=f(x)\)的导函数用\(f'(x)\)表示外，也可以使用分数形式表示，两者是等效的:

\[ f'(x) = \frac{dy}{dx} \]

导数的性质

\[ \{f(x) + g(x)\}' = f'(x) + g'(x) \]

\[ \{cf(x)\}' = cf'(x)\quad{（c为常数）} \]

上面性质可以总结为和的导数为导数的和，常数倍的导数为导数的常数倍。

当函数是分数形式时候，存在下面的求导公式

\[ \{\frac{1}{f(x)}\}' = -\frac{f'(x)}{\{f(x)\}^2} \]

注意：上面公式中\(f(x)\)不取0值。

Sigmoid函数的导数

Sigomod函数的定义如下所示：

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

它的导数为：

\[ \sigma'(x) = \sigma(x)(1- \sigma(x)) \]

证明：将\(1+e^{-x}\)带入上面分数形式的函数导数公式中，我们得到：

\[ \begin{aligned} \sigma'(x) &= - \frac{(1+ e^{-x})'}{(1+e^{-x})^2} \\ &= \frac{e^{-x}}{(1+ e^{-x})^2}\\ &= \frac{1 + e^{-x} -1}{(1+e^{-x})^2} \\ &= \frac{1}{1 + e^{-x}} - \frac{1}{(1+ e^{-x})^2}\\ &= \sigma(x) - \sigma(x)^2\\ &= \sigma(x)(1- \sigma(x)) \end{aligned} \]

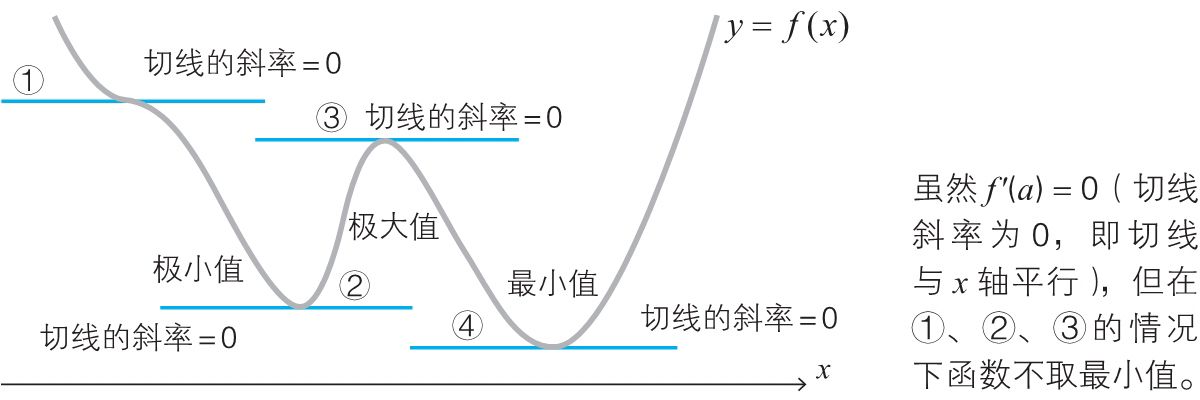
最小值条件

当函数\(f(x)\)在\(x=a\)处取得最小值时，\(f'(a) = 0\)。从下图中，我们可以看出\(f'(a) = 0\)是函数\(f(x)\)在\(x = a\)处取得最小值的必要条件,但不是充条件。

[!note] 笔记 已知命题\(p\)、\(q\),由\(p\)可以推出\(q\)，则\(q\)称为\(p\)的必要条件。

偏导数

多变量函数

有两个以上的自变量的函数称为多变量函数。单变量函数用\(f(x)\)表示，同理我们可以用\(f(x, y)\)表示有两个自变量\(x\),\(y\)的函数。以此类推，由\(n\)个自变量\(x_1\),\(x_2\),\(\cdots\),\(x_n\)的函数，可以记作\(f(x_1,x_2,\cdots,x_n)\)。

偏导数定义

关于某个特定变量的导数，称为偏导数（partial derivative)。

考虑有两个变量\(x\)、\(y\)的函数\(z = f(x, y)\),关于\(x\)的偏导数可以用下面符号表示:

\[ \frac{\partial z}{\partial x} = \frac{\partial f(x,y)}{\partial x} = \lim_{\Delta x\to 0}\frac{f(x + \Delta x, y) - f(x,y）}{\Delta x} \]

同样关于\(y\)的偏导数如下表示：

\[ \frac{\partial z}{\partial y} = \frac{\partial f(x,y)}{\partial y} = \lim_{\Delta y\to 0}\frac{f(x , y+\Delta y) - f(x,y)}{\Delta y} \]

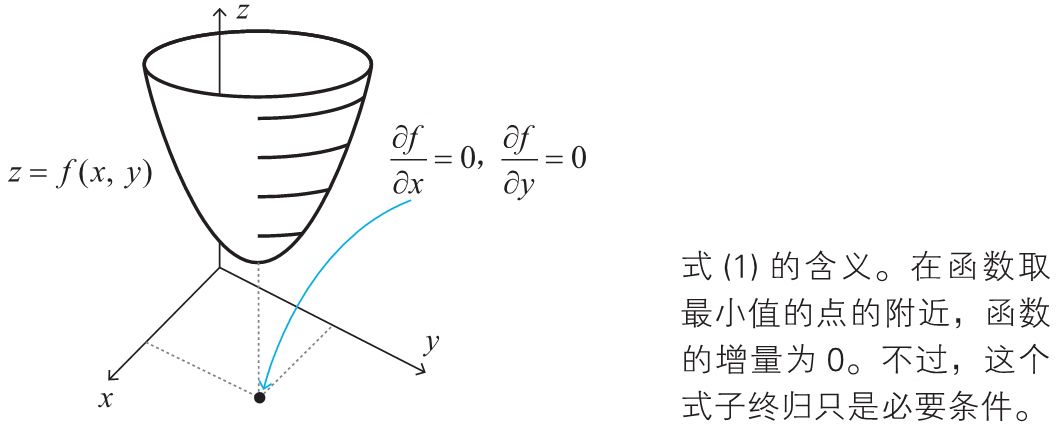
多变量函数的最小值条件

对于函数\(z = f(x, y)\)取得最小值的必要条件是\(\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0\)。

例子： 求函数\(z = x^2 + y ^2\)取得最小值时\(x\),\(y\)的值。

首先，我们来求关于\(x\),\(y\)的偏导数。

\[ \frac{\partial z}{\partial x} = 2x, \frac{\partial z}{\partial y} = 2y \]

根据多变量函数取得最小值的的必要条件，该函数取得最小值的必要条件是\(x=0, y=0\)，此时函数值\(z\)为0。由于\(z= x^2 + y^2 \ge 0\),所以可以得出函数值0就是该函数的最小值。

例子： 当\(x^2 + y^2 = 1\)时，求\(x+y\)的最小值。

在实际的最小值问题中，有时会对变量附加约束条件，比如这个题目。这种情况下我们可以使用[[拉格朗日乘数法]]。这个方法首先引入参数\(\lambda\),创建下面的函数\(\mathcal{L}\)。

\[ \mathcal{L} = f(x, y) - \lambda g(x, y) = (x + y) - \lambda(x^2 + y^2 -1) \]

利用多元函数最小值必要条件，我们得到：

\[ \frac{\partial \mathcal{L} }{\partial x} = 1 - 2\lambda x = 0, \frac{\partial \mathcal{L} }{\partial y} = 1 - 2\lambda y = 0, \]

根据上面式子，以及约束条件\(x^2 + y^2 = 1\)，我们计算得到\(x = y = \lambda = \pm\frac{1}{\sqrt{2}}\)。

因此，当\(x = y = -\frac{1}{\sqrt{2}}\)时，\(x+y\)取得最小值\(-2\)。

链式法则

复合函数

已知函数\(y = f(u)\),当\(u\)表示为\(u = g(x)\)时，\(y\)作为\(x\)的函数可以表示为形如\(y = f(g(x))\)的嵌套函数（\(u\)和\(x\)表示多变量）。这时，嵌套结构的函数\(f(g(x))\)称为\(f(u)\)和\(g(x)\)的复合函数。

例1：函数\(z = (2-y)^2\)是函数\(u = 2 - y\)和函数\(z = u^2\)的复合函数。

例2：对于多个输入\(x_1,x_2,\cdots,x_n\),将\(a(x)\)作为激活函数，求神经单元的输出\(y\)的过程如下表示：

\[ y = a(w_1x_1 + w_2x_2 + \cdots + w_nx_n + b) \]

\(w_1,w_2,\cdots,w_n\)为各输入对应的权重，\(b\)为神经单元的偏置。这个输出函数是如下的\(x_1,x_2,\cdots,x_n\)的一次函数\(f\)和激活函数\(a\)的复合函数。

\[ \left \{ \begin{array}{l} % l 靠左、c 居中、r 靠右 z = f(x_1, x_2, \cdots, x_n) = w_1x_1 + w_2x_2 + \cdots + w_nx_n +b\\\\ y = a(z) \end{array} \right. \]

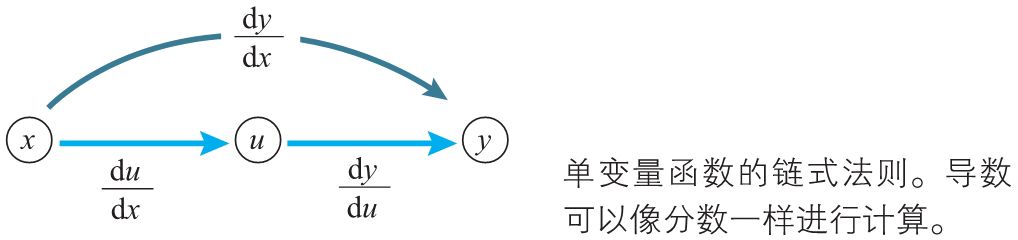
单变量函数的链式法则

已知单变量函数\(y = f(u)\)，当\(u\)表示为单变量函数\(u = g(x)\)时，复合函数\(f(g(x))\)的导函数公式如下：

\[ \frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx} \]

这个公式称为单变量函数的复合函数求导公式，也称为链式法则。

例3：当\(y\)为\(u\)的函数，\(u\)为\(v\)的函数，\(v\)为\(x\)的函数时，那么:

\[ \frac{dy}{dx} = \frac{dy}{du}\frac{du}{dv}\frac{dv}{dx} \]

示例：对于\(x\)的函数\(y = \frac{1}{1 + e^{-(wx + b)}}(w, b为常数)\)求导.

我们设定一下函数：

\[ y = \frac{1}{1+ e^{-u}}, \quad u = wx +b \]

有前面的Sigmod函数的导函数公式可以得出：

\[ \frac{dy}{du} = y(1-y) \]

此外,由于\(\frac{du}{dx} =w\),所以可得：

\[ \frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx} = y(1-y)w = \frac{w}{1 + e^{-(wx+b)}}(1 - \frac{1}{1+ e^{-(wx+b)}}) \]

多变量函数的链式法则

在多变量函数的情况下，链式法则同样适用，但必须对相关的全部变量应用链式法则。

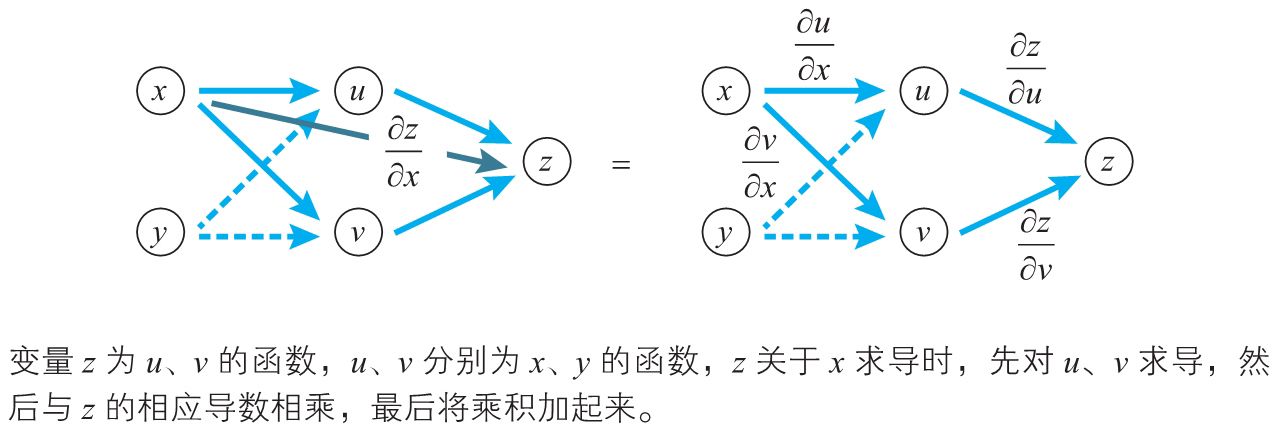
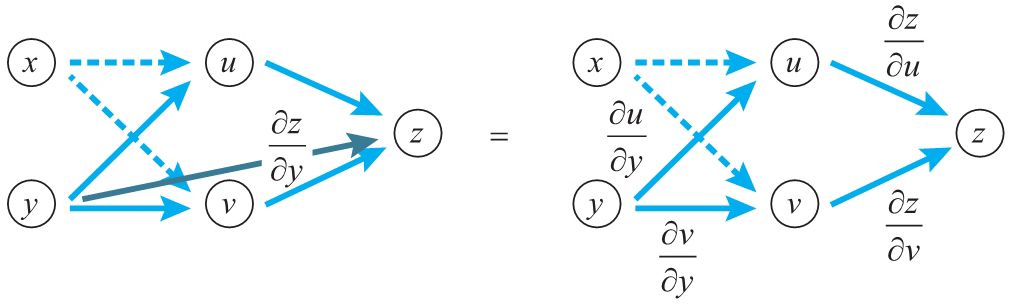
考察两个变量的情况。变量\(z\)为\(u\),\(v\)的函数，如果\(u\),\(v\)分别为\(x\),\(y\)的函数，则\(z\)为\(x\),\(y\)的函数，此时有下面公式：

\[ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial z}{\partial v}\frac{\partial v}{\partial x} \]

同理对\(y\)求导，也有下面公式：

\[ \frac{\partial z}{\partial y} = \frac{\partial z}{\partial u}\frac{\partial u}{\partial y} + \frac{\partial z}{\partial v}\frac{\partial v}{\partial y} \]

上面公式中各变量的关系图如下：

例5：当\(C = u^2 + v^2, u= ax+ by, v = px +qy\quad{a,b,p,q为常数}\)时，求函数\(C\)分别关于\(x\)和\(y\)的偏导函数。

\[ \begin{aligned} \frac{\partial C}{\partial x} &= \frac{\partial C}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial C}{\partial v}\frac{\partial v}{\partial x} \\\\ &= 2u \cdot a + 2v \cdot p \\\\ &= 2a(ax+ by) +2p(px + qy) \end{aligned} \]

\[ \begin{aligned} \frac{\partial C}{\partial y} &= \frac{\partial C}{\partial u}\frac{\partial u}{\partial y} + \frac{\partial C}{\partial v}\frac{\partial v}{\partial y} \\\\ &= 2u \cdot b + 2v \cdot q \\\\ &= 2b(ax+ by) +2q(px + qy) \end{aligned} \]

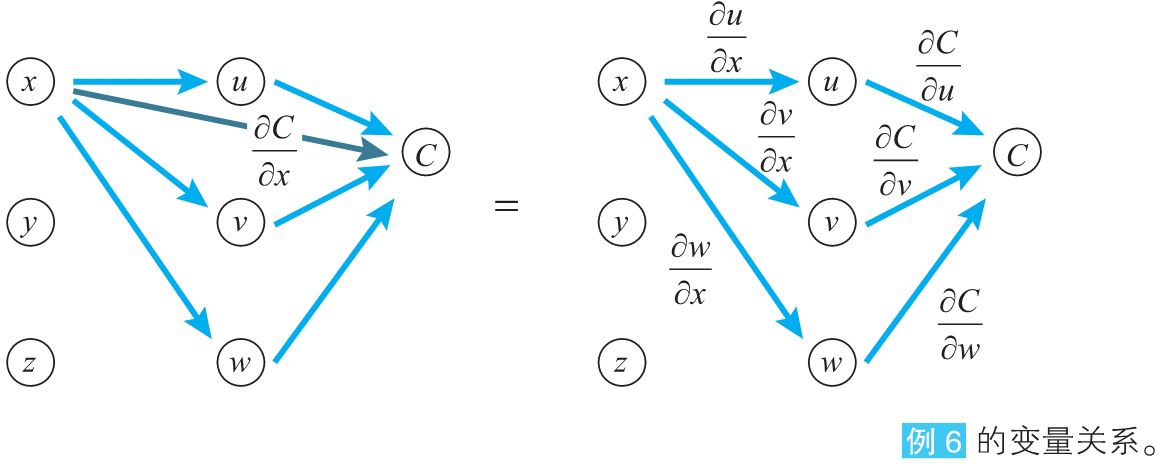
例6： 当\(C=u^2 + v^2 + w^2, u = a_1x + b_1y + c_1z, v = a_2x+ b_2y +c_2z, w=a_3x + b_3y+c_3\quad{(a_i,b_i,c_i为常数，i=1,2,3)}\)时请求\(C\)分别关于\(x\)、\(y\)的导函数。

\[ \begin{aligned} \frac{\partial C}{\partial x} &= \frac{\partial C}{\partial u}\frac{\partial u}{\partial x} + \frac{\partial C}{\partial v}\frac{\partial v}{\partial x} + \frac{\partial C}{\partial w}\frac{\partial w}{\partial x}\\\\ &= 2u\cdot a_1 + 2v\cdot a_2 + 2w \cdot a_3 \\\\ &= 2a_1(a_1x + b_1y + c_1z) + 2a_2(a_2x+ b_2y + c_2z) + 2a_3(a_3x + b_3y + c_3) \end{aligned} \]

多变量函数的近似公式

单变量函数的近似公式

从导函数的定义式：

\[ f'(x) = \lim_{\Delta x \to 0}\frac{f(x + \Delta x) - f(x)}{\Delta x} \]

上面定义式中\(\Delta x\)为“无限小的值”，如将它替换为“微小的值”，也不会造成很大的误差。因而，下面近似成立：

\[ f'(x) = \frac{f(x+\Delta x) - f(x)}{\Delta x} \]

将上式变形，可以得到单变量函数的近似公式:

\[ f(x + \Delta x) = f(x) + f'(x)\Delta x \quad{(\Delta x 为微小的数)}\quad{(1)} \]

例1： 当\(f(x) = e^x\)时，求\(x=0\)附近的近似公式。

根据单变量函数的近似公式，我们可以得到：

\[ e^{x+\Delta x} = e^x + e^x\Delta x \quad{(\Delta x为微小的值)} \]

取\(x=0\),重新将\(\Delta x\)替换为\(x\)，可得\(e^x = 1 + x\quad{(x为微小的值)}\)。

画出\(y=e^x\)与\(y=1+x\)图像，可以看出在\(x=0\)附近处，两者近乎重叠。

多变量函数的近似公式

如果\(x\)、\(y\)作微小的变化，那么函数\(z= f(x, y)\)的值变化可以用下面近似公式表示：

\[ f(x+\Delta x, y+ \Delta y) = f(x, y) +\frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x, y)}{\partial y}\Delta y \quad{(2)} \]

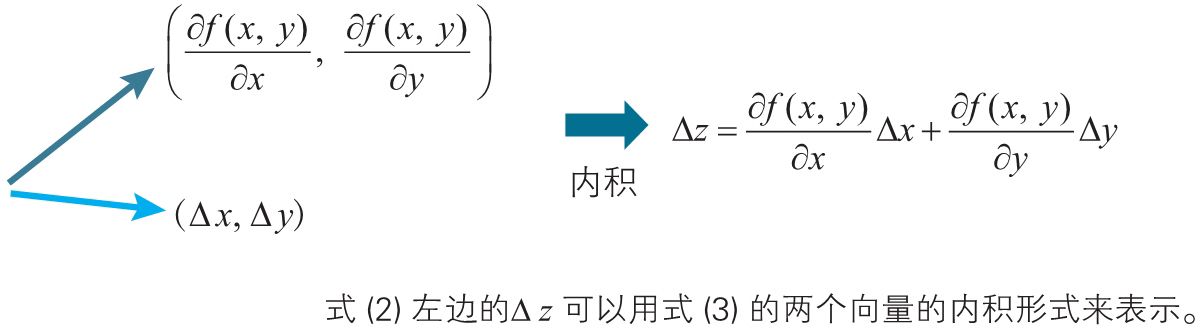
我们定义如下\(\Delta z\)：

\[ \Delta z = f(x+\Delta x, y+ \Delta y) - f(x, y) \]

根据式(2)我们可以得到：

\[ \Delta z = \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y\quad{(3)} \]

将式(3)推广到3个变量\(x, y, w\)函数时，近似公式如下：

\[ \Delta z = \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y + \frac{\partial z}{\partial w}\Delta w\quad{(4)} \]

近似公式的向量表示

三个变量的函数的近似公式(4)可以表示为如下两个向量的内积\(\nabla z \cdot \Delta x\)的形式。其中\(\Delta z\)、\(\Delta x\)分别如下：

\[ \nabla z = \left ( \begin{matrix} \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} & \frac{\partial z}{\partial w} \end{matrix} \right ) , \Delta x = (\Delta x, \Delta y, \Delta w) \]

泰勒展开式

将近似公式的一般化公式称为泰勒展开式。例如，在两个变量情况下，这个公式如下所示：

\[ \begin{aligned} f(x + \Delta x, y + \Delta y) &= f(x, y) + \frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \\ &+ \frac{1}{2!}\Bigl\{\frac{\partial ^2 f}{\partial x^2}(\Delta x)^2 + 2\frac{\partial ^2 f}{\partial x \partial y}\Delta x\Delta y + \frac{\partial^2f}{\partial y^2}(\Delta y)^2\Bigr\}\\ &+ \frac{1}{3!}\Bigl\{ \frac{\partial ^3f}{\partial x^3}(\Delta x)^3 + 3\frac{\partial ^3 f}{\partial x^2 \partial y}(\Delta x)^2\Delta y)+ 3\frac{\partial ^3 f}{\partial x \partial y^2}\Delta x(\Delta y)^2 + \frac{\partial ^3 f}{\partial y^3}(\Delta y)^3 \Bigr\}\\ &+ \cdots \end{aligned} \]

上面式子中，我们约定\(\frac{\partial ^2 f}{\partial x^2} = \frac{\partial}{\partial x}\frac{\partial f}{\partial x}, \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial }{\partial x}\frac{\partial f}{\partial y}\cdots\)。

在泰勒展开式中，取出前三项，就可得到式(2)。

梯度下降法

应用数学最重要的任务之一就是寻找函数取最小值的点。梯度下降法是著名的寻找最小值的点的方法。

梯度下降法的思路

根据前面的介绍函数\(z=f(x,y)\)取得的最小值的必要条件如下：

\[ \frac{\partial f(x, y)}{\partial x} = 0,\frac{\partial f(x, y)}{\partial y} =0 \quad{(1)} \]

这是因为，在函数取最小值的点处，就像葡萄酒杯的底部那样，与函数相切的平面变得水平。

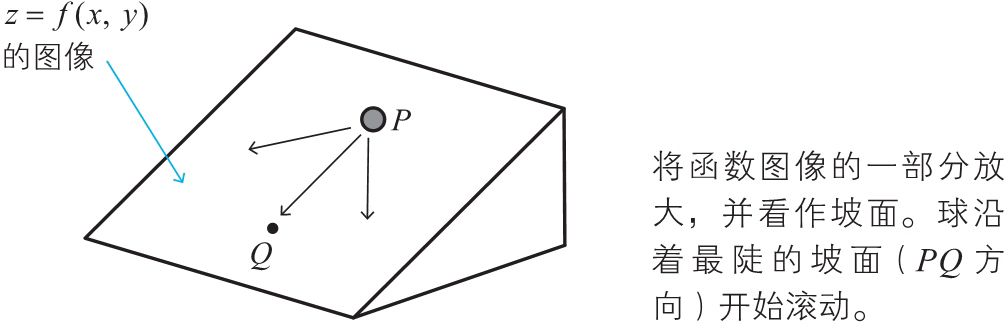
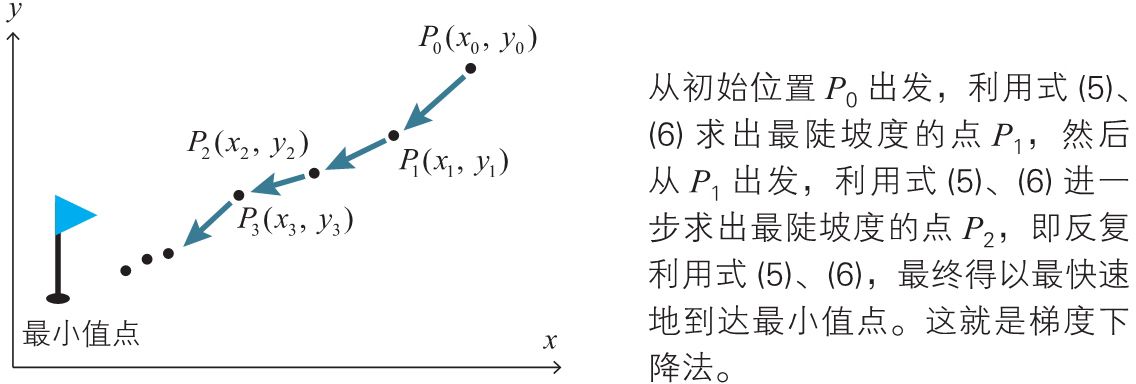
在实际问题中，联立方程式(1)通常不容易求解，这个时候梯度下降法出场了。该方法不直接求解式(1)的方程，而是通过慢慢地移动图像上的点进行摸索，从而找出函数的最小值。

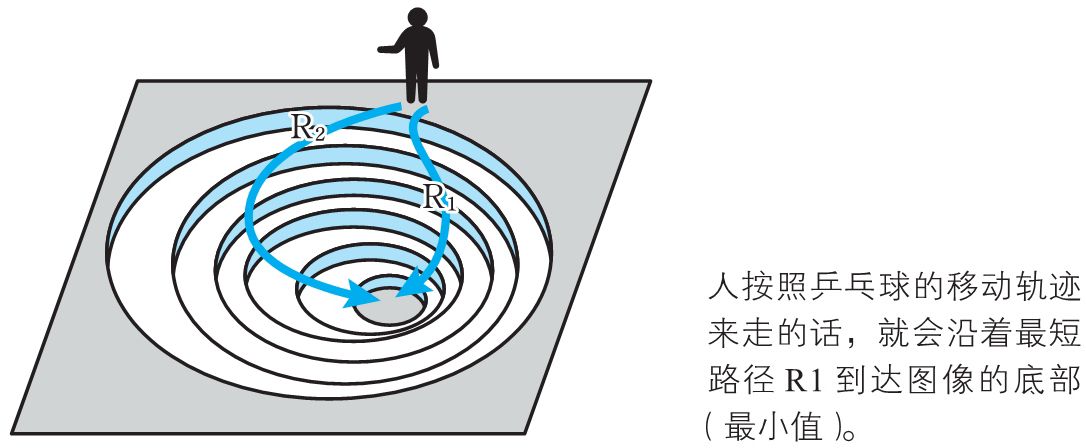
我们将图像看做斜坡，在斜坡上点\(P\)处放一个乒乓球，然后轻轻松开手，球会沿着最陡的坡面开始滚动，待球稍微前进一点后，把球止住，然后从止住的位置再次松手，乒乓球会从这个点再次沿着最陡的坡面开始滚动。

这个操作反复进行若干次后，乒乓球沿着最短的路径到达了图像的底部，也就是函数的最小值点。梯度下降法就模拟了这个球的移动过程。

如果将画出函数的登高线图，那么梯度下降法移动过程如下：

在数值分析领域，梯度下降法也称为最速下降法。这个名称表示沿着图像上的最短路径下降。

近似公式和内积关系

函数\(z = f(x, y)\)中，当\(x\)改变\(\Delta x\)，\(y\)改变\(\Delta y\)，函数\(f(x, y)\)的值变化\(\Delta z\),用如下公式表示：

\[ \Delta z = f(x + \Delta x, y+ \Delta y) - f(x, y) \]

根据近似公式，以下关系式成立：

\[ \Delta z = \frac{\partial f(x, y)}{\partial x}\Delta + \frac{\partial f(x,y)}{\partial y}\Delta y \quad{(2)} \]

而上面公式可以表示成下面的两个向量的内积：

\[ \left ( \begin{matrix} \frac{\partial f(x,y)}{\partial x} & \frac{\partial f(x,y)}{\partial w} \end{matrix} \right ) \cdot (\Delta x, \Delta y) \quad(3) \]

根据前面介绍的柯西-施瓦茨不等式，我们知道两个固定大小的非零向量\(a\),\(b\)，当\(b\)的方向与\(a\)相反时，内积\(a\cdot b\)取最小值，即\(b\)满足以下条件式时，可以使用内积\(a\cdot b\)取最小值：

\[ b = -ka\quad{(k为正的常数)}\quad{(4)} \]

二变量函数的梯度下降法的基本式

根据式 (4)，当两个向量方向相反时，内积取最小值。也就是说，当式 (3) 的两个向量的方向恰好相反时，式(2) 的\(\Delta z\)达到最小（即减小得最快）​。

于是，我们可以知道，从点\((x, y)\)向点\((x+\Delta x, y+\Delta y)\)移动时，满足下面关系式时，函数\(z = f(x, y)\)减小的最快，这个关系式就是二变量函数的梯度下降法的基本式：

\[ (\Delta x, \Delta y) = -\eta(\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y}) \quad{(\eta 为正的微小常数)} \quad(5) \]

上面基本式中的\((\frac{\partial f(x, y)}{\partial x}, \frac{\partial f(x, y)}{\partial y})\)称为函数\(f(x, y)\)在点\((x, y)\)处的梯度（gradient),这个名字来自于它给出了最陡的坡度方向。

利用关系式(5),如果从点\((x,y)\)向点\((x+\Delta x, y + \Delta y)\)移动(6),就可以从图像上点\((x, y)\)的位置最快速地下坡。

梯度下降法的用法

要寻找函数的最小值，可以利用式 (5) 找出减小得最快的方向，沿着这个方向依照上述 (6) 稍微移动。在移动后到达的点处，再次利用式 (5) 算出方向，再依照上述 (6) 稍微移动。通过反复进行这样的计算，就可以找到最小值点。

二变量函数的梯度下降法的基本式 (5) 可以很容易地推广到三个变量以上的情形。当函数 \(f\) 由 \(n\) 个自变量 \(x_1,x_2, \cdots, x_n\) 构成时，梯度下降法的基本式 (5) 可以像下面这样进行推广。

设\(\eta\)为正的微小常数，变量\(x_1,x_2,\cdots, x_n\), 改变为\(x_1+\Delta x_1,x_2 + \Delta x_2, \cdots , x_n + \Delta x_n\),当满足以下关系式时，函数\(f\)减小得最快。

\[ (\Delta x_1, \Delta x_2, \cdots, \Delta x_n) = -\eta(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n})\quad(7) \]

其中\((\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n})\)称为函数\(f\)在点\((x_1,x_2,\cdots, x_n)\)处的梯度。

利用这个关系式 (7)，如果

\[ 从点 (x_1, x_2, \cdots, x_n 向点 (x_1 + \Delta x_1, x_2 + \Delta x_2, \cdots, x_n +\Delta x_n)移动\quad(8) \]

就能够沿着函数减小得最快的方向移动。因此，反复依照上述 (8) 来移动，就能够在 \(n\) 维空间中算出坡度最陡的方向，从而找到最小值点。这就是 \(n\) 变量情况下的梯度下降法。

为了简洁表示梯度，这里引入了\(\nabla\)符号，\(\nabla\)称为哈密顿算子，它源于希腊竖琴的形象,其定义如下：

\[ \nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n}) \]

于是公式(7)可以表示为如下：

\[ (\Delta x_1, \Delta x_2, \cdots, \Delta x_n) = -\eta\nabla f \quad{(\eta 为正的微小常数)} \]

其中 \((\Delta x_1, \Delta x_2, \cdots, \Delta x_n)\)称为位移向量,记为\(\Delta x\)。

利用这个位移向量，梯度下降法的基本式 (7) 可以更简洁地表示：

\[ \Delta x = -\eta\nabla f \quad{(n为正的微小常数)} \]

\(\eta\)的含义

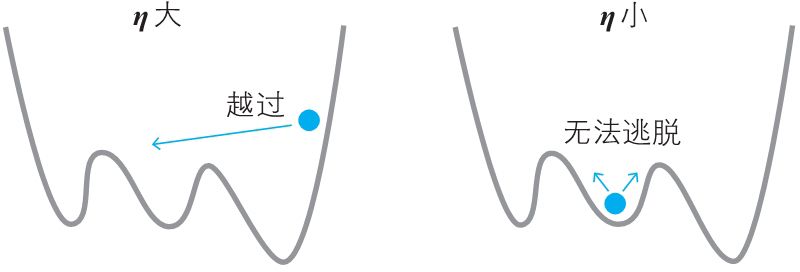
\(\eta\) 只是简单地表示正的微小常数。从式 (5) 的推导过程可知，\(\eta\) 可以看作人移动时的“步长”​，根据 \(\eta\) 的值，可以确定下一步移动到哪个点。如果步长较大，那么可能会到达最小值点，也可能会直接跨过了最小值点（左图）​。而如果步长较小，则可能会滞留在极小值点（右图）​。

在神经网络的世界中，\(\eta\) 称为学习率。遗憾的是，它的确定方法没有明确的标准，只能通过反复试验来寻找恰当的值。

最优化问题和回归分析

在为了分析数据而建立数学模型时，通常模型是由参数确定的。在数学世界中，最优化问题就是如何确定这些参数。

从数学上来说，确定神经网络的参数是一个最优化问题，具体就是对神经网络的参数（即权重和偏置）进行拟合，使得神经网络的输出与实际数据相吻合。

回归分析

由多个变量组成的数据中，着眼于其中一个特定的变量，用其余的变量来解释这个特定的变量，这样的方法称为回归分析。

一元线性回归分析是以两个变量组成的数据为考察对象的。一元线性回归分析是最简单的回归分析。

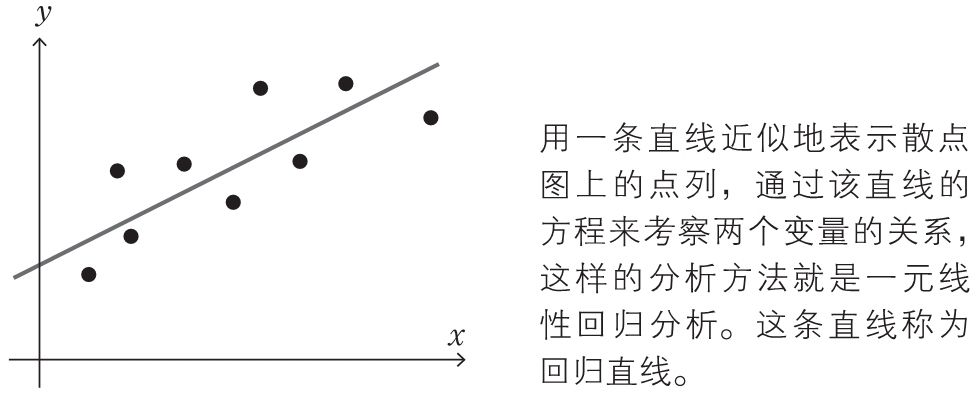
一元线性回归分析是用一条直线近似地表示下图所示的散点图上的点列，通过该直线的方程来考察两个变量之间的关系。这条近似地表示点列的直线称为回归直线。

这条回归直线用一次关系式表示如下：

\[ y = px + q \quad{(p, q 为常数)} \]

这个式子称为回归方程，其中\(p\)称为回归系数，\(q\)称为截距。

示例

下面以身高为自变量，体重为因变量的回归方程为例子：

\[ y = px + q \quad {(p,q为常数)} \]

那么对于第\(k\)个学生，他/她的身高记为为\(x_k\),体重记为\(y_k\)，那么第\(k\)个学生的回归分析预测的体重值\(\hat y_k\)为：

\[ \hat y_k = px_k + q \]

那么实际体重\(y_k\)与预测值\(\hat y_k\)的误差如下，记为\(e_k\):

\[ e_k = y_k - (px_k + q) \]

考虑到\(e_k\)有正负的情况，我们使用平方误差来误差情况：

\[ C_k = \frac{1}{2}(e_k)^2 = \frac{1}{2}\{y_k - (px_k + q)\}^2 \]

注意：上式中\(\frac{1}{2}\)非必须，这是因为后面处理梯度时候，乘以平方导数中的2倍的时候，恰好为1，好处理些。

上面\(C_k\)只是考虑一个数据点的误差，对于考察整体的误差，我们可以把所有点的平方误差加起来，记为\(C_T\):

\[ C_T = C_1 + C_2 + \cdots + Cn \]

最终的回归分析的目的就是确定常数\(p\),\(q\)的值，使得误差总和\(C_T\)值最小。根据前面介绍的[[#多变量函数的最小值条件]]，\(C_T\)取最小值时候，有:

\[ \frac{\partial C_T}{\partial q} = 0, \frac{\partial C_T}{\partial q} = 0 \]

将数据集代入回归方程中，计算得到所有预测值，再将真实的值带入上面梯度方程中，就可以得到最佳的参数\(p\),\(q\)。

在最优化方面，误差总和\(C_T\)可以称为“误差函数”、​“损失函数”​、“代价函数”等。这种利用平方误差的总和\(C_T\)进行最优化的方法称为最小二乘法。

[!warning] 注意 之所以不使用误差函数（error function）​、损失函数（lost function）的叫法，是因为它们的首字母容易与神经网络中用到的熵（entropy）​、层（layer）的首字母混淆。

评论