深度学习入门：基于Python的理论与实现¶
Chap1: Python入门¶
Matplotlib的使用¶
Sin函数曲线¶
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.1) # 以0.1为单位，生成0到6的数据
y = np.sin(x)
plt.plot(x, y)
plt.show()
Sin/Cos函数曲线¶
x = np.arange(0, 6, 0.1)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos") # 虚线
plt.xlabel("x") # x轴标签
plt.ylabel("y") # y轴标签
plt.title("sin & cos") # 标题
plt.legend()
plt.show()
显示图片¶
from matplotlib.image import imread
from PIL import Image
from io import BytesIO
import requests
# imread("local_image_file")
url = "https://static.cyub.vip/images/202410/lena.png"
response = requests.get(url)
img = Image.open(BytesIO(response.content))
plt.imshow(img)
plt.show()
ReLU曲线¶
ReLU（Rectified Linear Unit）激活函数的曲线。ReLU函数定义为：
$$ f(x)=max(0,x) $$
这意味着当输入x小于0时，输出为0；当输入x大于或等于0时，输出为x的值。
# 定义ReLU函数
def relu(x):
return np.maximum(0, x)
# 生成x值
x = np.linspace(-10, 10, 1000)
# 计算ReLU函数的y值
y = relu(x)
# 绘制ReLU曲线
plt.plot(x, y)
plt.title('ReLU Activation Function')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子
np.random.seed(0)
# 生成随机数据
num_samples = 100
x1 = np.random.rand(num_samples)
x2 = np.random.rand(num_samples)
# 设置权重和偏置
w1 = 2
w2 = -1
b = 0.5
# 计算输出
y = np.where(w1*x1 + w2*x2 + b > 0, 1, 0)
# 绘制散点图
plt.scatter(x1[y==1], x2[y==1], label='Positive')
plt.scatter(x1[y==0], x2[y==0], label='Negative')
# 绘制决策边界
x_plot = np.linspace(0, 1, 100)
y_plot = -(w1/w2)*x_plot - b/w2
plt.plot(x_plot, y_plot, 'r--', label='Decision Boundary')
# 设置坐标轴标签和图例
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
# 显示图像
plt.show()
Chap2: 感知机¶
感知机（perceptron）是由美国学者 Frank Rosenblatt 在 1957 年提出来的。感知机接收多个输入信号，输出一个信号。
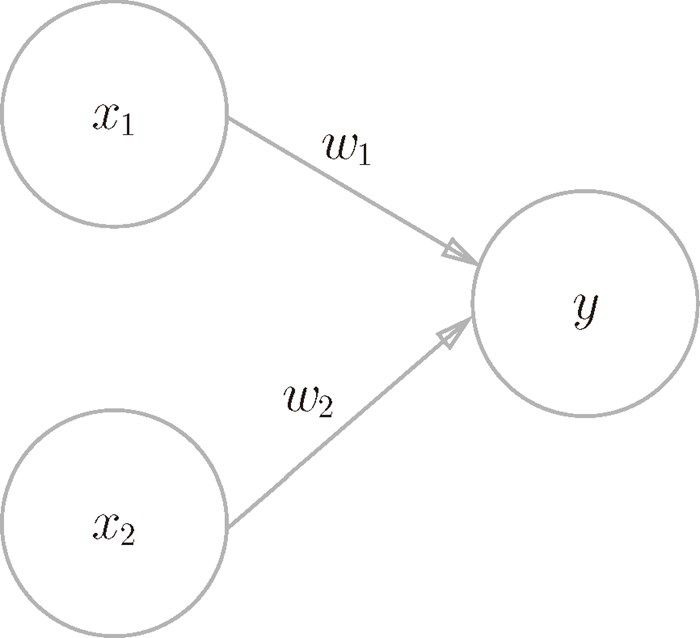
下图中是一个接收两个输入信号的感知机的例子。x1、x2 是输入信号，y 是 输 出 信 号，w1、w2 是 权 重（w 是 weight 的 首 字 母）。图 中 的 ○ 称 为“神经元”或者“节点”。输入信号被送往神经元时，会被分别乘以固定的权重（w1x1、w2x2）。神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出 1。这也称为“神经元被激活”。这里将这个界限值称为阈值，用符号 θ 表示。
感知机的多个输入信号都有各自固有的权重，这些权重发挥着控制各个信号的重要性的作用。也就是说，权重越大，对应该权重的信号的重要性就越高。
数学公式：
$$ f(x)= \begin{cases} 0 &&(w_1 x_1 + w_2 x_2) \le \theta\\\\ 1 &&(w_1 x_1 + w_2 x_2) \gt \theta \end{cases} $$
简单逻辑电路¶
与门¶
与门(AND gate)仅在两个输入均为 1 时输出 1，其他时候则输出 0。输入信号和输出信号的对应表称为“真值表。与门的真值表：
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
如果用感知机来实现上面的与门，其中$w1$, $w2$, $\theta$的可能取值有：
(0.5, 0.5, 0.7)
(0.5, 0.5, 0.8)
等无穷多。
感知机实现¶
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2 * w2
if tmp <= theta:
return 0
else:
return 1
AND(0, 0), AND(1, 0), AND(1, 0), AND(1, 1)
(0, 0, 0, 1)
权重与偏置¶
将$\theta$换成 $-b$之后，我们可以得到以下数学公式：
$$ f(x)= \begin{cases} 0 &&(b + w_1 x_1 + w_2 x_2) \le 0\\\\ 1 &&(b + w_1 x_1 + w_2 x_2) \gt 0 \end{cases} $$
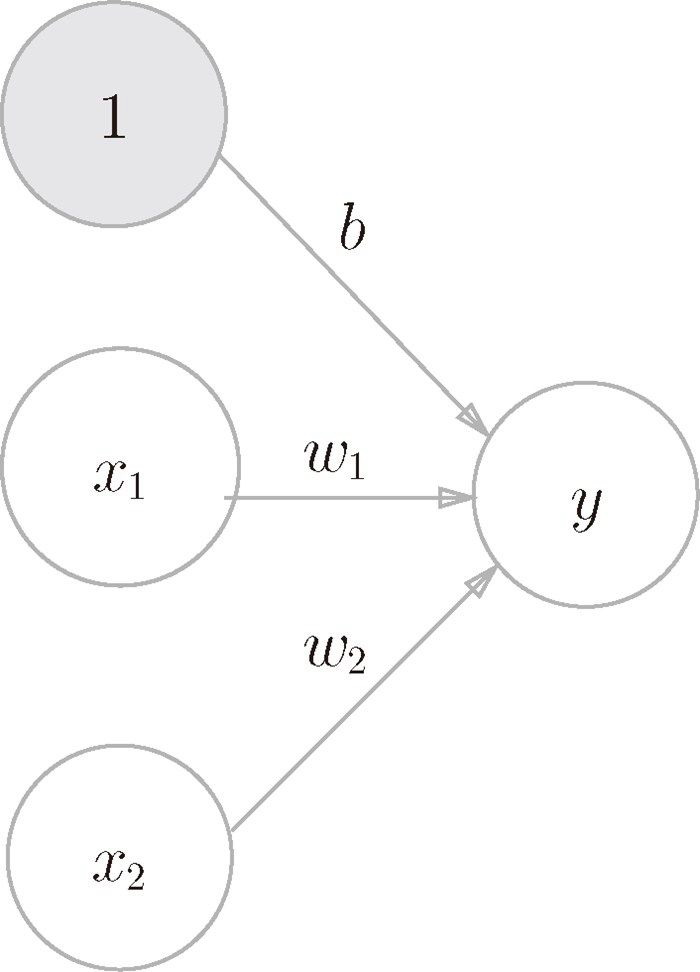
虽然有一个符号不同，但表达的内容是完全相同的。此处，b 称为偏置，w1 和 w2 称为权重。感知机会计算输入信号和权重的乘积，然后加上偏置，如果这个值大于 0 则输出 1，否则输出 0。w1 和 w2 是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为 1 的程度）的参数。
我们可以把偏置当做成权重为b的输入信号1：
import numpy as np
x = np.array([0, 1]) # 输入
w = np.array([0.5, 0.5]) # 权重
b = -0.7 # 偏置
np.sum(x * w)
np.float64(0.5)
np.sum(x * w) + b
np.float64(-0.19999999999999996)
基于权重和偏置的实现¶
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp<=0:
return 0
else:
return 1
AND(0, 0), AND(1, 0), AND(1, 0), AND(1, 1)
(0, 0, 0, 1)
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
NAND(0, 0), NAND(1, 0), NAND(1, 0), NAND(1, 1)
(1, 1, 1, 0)
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
OR(0, 0), OR(1, 0), OR(1, 0), OR(1, 1)
(0, 1, 1, 1)
感知机的局限性¶
感知机是无法实现这个异或门的。
异或门¶
异或门（XOR gate）也被称为逻辑异或电路。仅当 $x_1$ 或 $x_2$ 中的一方为1 时，才会输出 1。异或门的真值表：
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
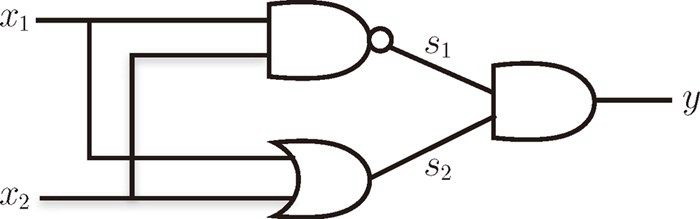
多层感知机¶
感知机可以通过多层叠加实现异或门。下面是与门、与非门、或门的逻辑符号。
下面是通过组合与门、与非门、或门来实现异或门：
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
XOR(0, 0), XOR(1, 0), XOR(1, 0), XOR(1, 1)
(0, 1, 1, 0)
从上面可以看到与门、或门是单层感知机，而异或门是 2 层感知机。叠加了多层的感知机也称为多层感知机（multi-layered perceptron）。下图使用感知机表示异或门：
该图中感知机总共由 3 层构成，但是因为拥有权重的层实质上只有 2 层（第 0 层和第 1 层之间，第 1 层和第 2 层之间），所以称为“2 层感知机”。不过，有的文献认为图 2-13 的感知机是由 3 层构成的，因而将其称为“3 层感知机”
Chap3 神经网络¶
感知机的局限性：
即便是计算机进行的复杂处理，感知机（理论上）也可以将其表示出来。坏消息是，设定权重的工作，即确定合适的、能符合预期的输入与输出的权重，现在还是由人工进行的。
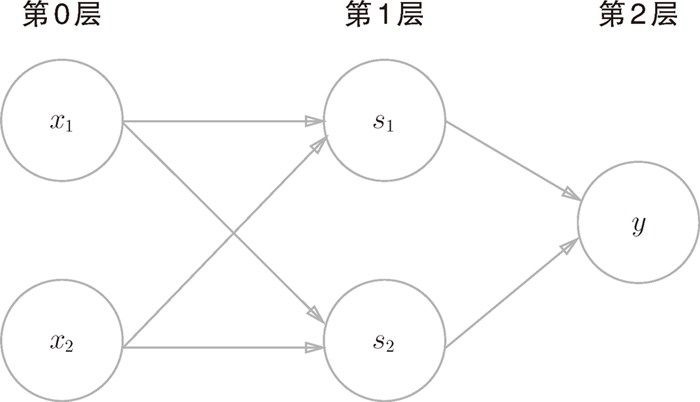
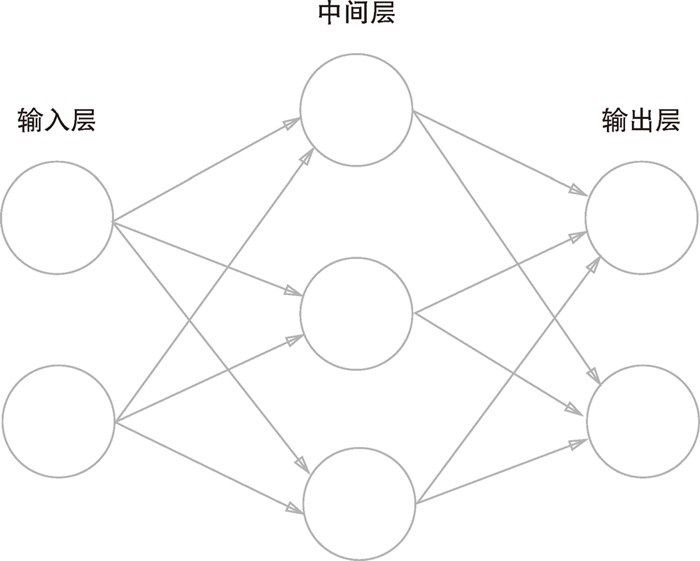
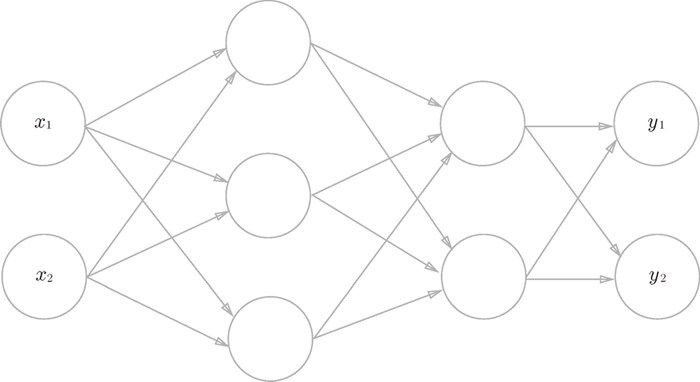
神经网络例子¶
神经网络中最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层。中间层有时也称为隐藏层。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同）肉眼看不见。我们把输入层到输出层依次称为第 0 层、第1 层、第 2 层。下面图中是3层神经元构成，因为只有2层神经元有权重，因此将其称为”2层网络“，但有些会根据构成网络的层数，把它称为”3层网络“。
激活函数¶
$$ y = \begin{cases} 0 && (b + w_1 x_1 + w_2 x_2) \le 0\\\\ 1 &&(b + w_1 x_1 + w_2 x_2) + b \gt 0 \end{cases} $$
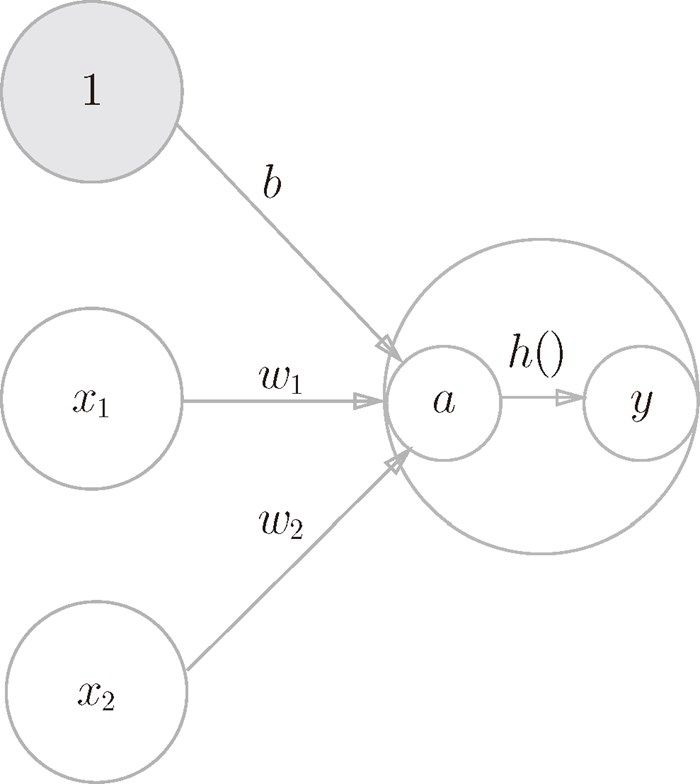
将上面感知机函数进行简化：
$$ a = b + w_1 x_1 + w_2 x_2 $$
$$ y = h(a) $$
其中$b + w_1 x_1 + w_2 x_2$是输入信号总和，可以看出一个整体$x$，进一步简化：
$$ y = h(x) = \begin{cases} 0 && x \le 0\\\\ 1 && x \gt 0 \end{cases} $$
上面公式中x是输入信号的总和，y输出信号。函数 $h(x)$ 称为激活函数（activation function）。激活函数用于将将输入信号的总和转换为输出信号，它决定了如何来激活输入信号的总和。
神经元经过激活函数的过程：
信号的加权总和为节点 a(节点即神经元），然后节点 a 被激活函数 $h()$ 转换成节点 y
上面的激活函数 $h(x)$ 是一个 阶跃函数。阶跃函数指的是以阈值为界，一旦输入超过阈值，就切换输出。
阶跃函数¶
阶跃函数实现¶
# 建议版本阶跃函数实现：只支持浮点数
def setp_function(x):
if x > 0:
return 1
else:
return 0
# 进阶版本阶跃函数：支持Numpy数组
def step_funcion(x):
y = x > 0
return y.astype(int) # 原书中是np.int，现在已放弃了
x = np.array([-1.0, 1.0, 2.0])
x
array([-1., 1., 2.])
y = x > 0
y
array([False, True, True])
y.astype(int)
array([0, 1, 1])
阶跃函数图形¶
def step_function(x):
return np.array(x >0, dtype=int)
def step_function_img():
x = np.arange(-8.0, 8.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.xlabel('x')
plt.ylabel('step_function(x)')
# plt.grid(True)
plt.show()
step_function_img()
sigmoid函数¶
$$ $$ \begin{aligned} h(x) \ \ & = \ \ \frac{1}{1\ \ \ \ + \ \ \ \ exp(-x)} \\ \\ &= \frac{1}{1\ \ \ \ + \ \ \ \ e^{-x}} \end{aligned} $$ $$
上面公式中$exp(-x)表示$e^{-x}$，其中e是纳皮尔常数。
sigmod函数实现¶
# sigmoid函数实现
def sigmoid(x):
return 1/(1 + np.exp(-x))
sigmoid函数图形¶
# sigmoid函数 测试
x = np.array([-1, 1.0, 2.0])
sigmoid(x)
array([0.26894142, 0.73105858, 0.88079708])
def sigmoid_img():
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴范围
# plt.title("sigmoid function")
plt.title('Sigmoid Activation Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()
# sigmoid 函数图像
sigmoid_img()
阶跃函数与sigmoid函数比较¶
阶跃函数和 sigmoid函数虽然在平滑性上有差异，但是如果从宏观视角，可以发现它们具有相似的形状， 它们都是非线性函数。实际上，两者的结构均是“输入小时，输出接近 0（为 0）；随着输入增大，输出向 1 靠近（变成 1）”。也就是说，当输入信号为重要信息时，阶跃函数和 sigmoid 函数都会输出较大的值；当输入信号为不重要的信息时，两者都输出较小的值。还有一个共同点是，不管输入信号有多小，或者有多大，输出信号的值都在 0 到 1 之间。
x = np.arange(-10.0, 10.0, 0.1)
y1 = sigmoid(x)
y2 = step_function(x)
plt.plot(x, y1)
plt.plot(x, y2, 'k--')
plt.ylim(-0.1, 1.1) #指定图中绘制的y轴的范围
plt.show()
神经网络的激活函数为什么不能使用线性函数？¶
线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐 藏 层 的 神 经 网 络”。这 里 我 们 考 虑 把 线 性 函 数 $h(x) = cx$ 作 为 激 活函 数，把 $y(x) = h(h(h(x)))$ 的 运 算 对 应 3 层 神 经 网 络 A。这 个 运 算 会 进 行 $y(x) = c × c × c × x$ 的乘法运算，但是同样的处理可以由 $y(x) = ax$（注意，$a = c^3$）这一次乘法运算（即没有隐藏层的神经网络）来表示。可以看到，使用线性函数时，无法发挥多层网络带来的优势。
ReLU函数¶
ReLU 函数在输入大于 0 时，直接输出该值；在输入小于等于 0 时，输出 0。ReLU 函数可以表示为下面的式：
$$ h(x) = \begin{cases} x && (x \gt 0)\\\\ 0 && (x \le 0) \end{cases} $$
ReLu函数实现¶
def ReLu(x):
return np.maximum(0, x)
ReLu函数图形¶
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()
多维数组的运算¶
数字排成一列的集合、排成长方形的集合、排成三维状或者（更加一般化的）N 维状的集合都称为 多维数组。对于二维数组，也成为矩阵（matrix），也有称为张量。
import numpy as np
A = np.array([1, 2, 3, 4]) # 一维数组
print(A) # 打印数组A
print(np.ndim(A)) # 打印数组A维度
print(A.shape) # 打印数组A形状，由于A是一维数组，所以元祖的第二个元素为空。
[1 2 3 4] 1 (4,)
B = np.array([[1, 2], [3, 4], [5, 6]])
print(B)
[[1 2] [3 4] [5 6]]
np.ndim(B)
2
B.shape # 3是B的第0维，2是B的第二维
(3, 2)
矩阵的乘法¶
矩阵的乘法(也叫乘积，也称为点积）是通过左边矩阵的行（横向）和右边矩阵的列（纵向）以对应元素的方式相乘后再求和而得到的。
对于矩阵A 和 矩阵 B的乘法：
$$ \left\{ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right\} \times \left\{ \begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix} \right\} = \left\{ \begin{matrix} (1 \times 5 + 2 \times 7) & (1 \times 6 + 2 \times 8) \\ (3 \times 5 + 4 \times 7) & (3 \times 6 + 4 \times 8) \end{matrix} \right\} = \left\{ \begin{matrix} 19 & 22 \\ 43 & 50 \end{matrix} \right\} $$
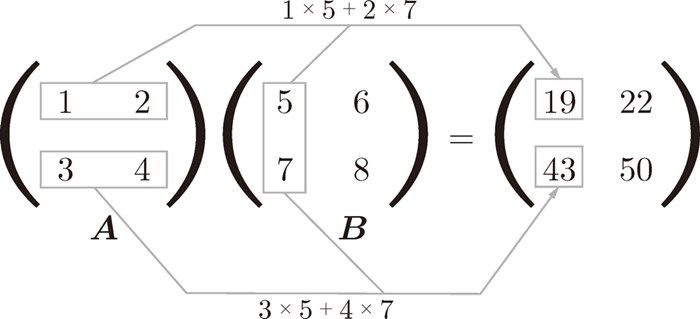
可以用下图表示：
从上面可以看到： A 的第 1 行和 B 的第 1 列的乘积结果是新数组的第 1 行第 1 列的元素，A 的第 2 行和 B 的第 1 列的结果是新数组的第 2 行第 1列的元素。Python 代码实现：
A = np.array([[1, 2], [3, 4]])
A.shape
(2, 2)
B = np.array([[5, 6], [7, 8]])
B.shape
(2, 2)
np.dot(A, B)
array([[19, 22],
[43, 50]])
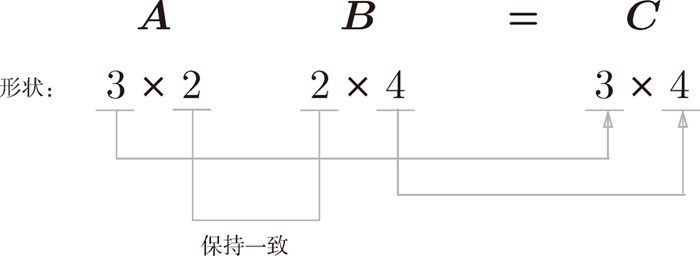
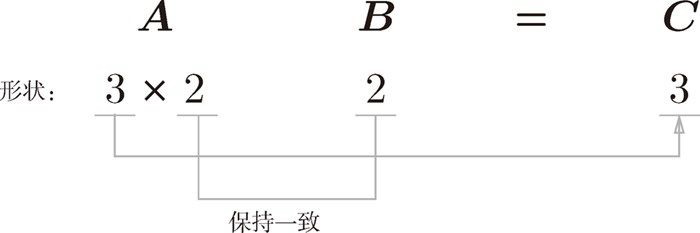
矩阵 A与矩阵 B计算时候必须满足矩阵 A 的第 1 维的元素个数（列数）必须和矩阵 B 的第 0 维的元素个数（行数）相等。即使其中一个是一维数组，也要保持一致。
下图中(3 x 2) x (2 x 4)是可以进行乘积运算的：
A = np.array([[1, 2], [3, 4], [5, 6]])
A.shape
(3, 2)
B = np.array([[7,8,9,10],[11, 12, 13, 14]])
B.shape
(2, 4)
np.dot(A, B)
array([[ 29, 32, 35, 38],
[ 65, 72, 79, 86],
[101, 112, 123, 134]])
下图中(3 x 2) x (2) 也是可以进行乘积运算的：
A = np.array([[1, 2], [3, 4], [5, 6]])
A.shape
(3, 2)
B = np.array([7, 8])
B.shape
(2,)
np.dot(A, B)
array([23, 53, 83])
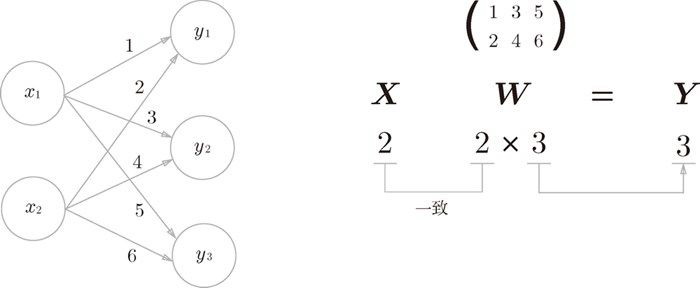
神经网络的内积¶
下图演示了神经网络的乘积运算(只考虑了权重，忽略了偏置和激活函数）：
X = np.array([1, 2])
X.shape
(2,)
W = np.array([[1, 3, 5], [2, 4, 6]])
print(W)
print(W.shape)
[[1 3 5] [2 4 6]] (2, 3)
Y = np.dot(X, W)
Y
array([ 5, 11, 17])
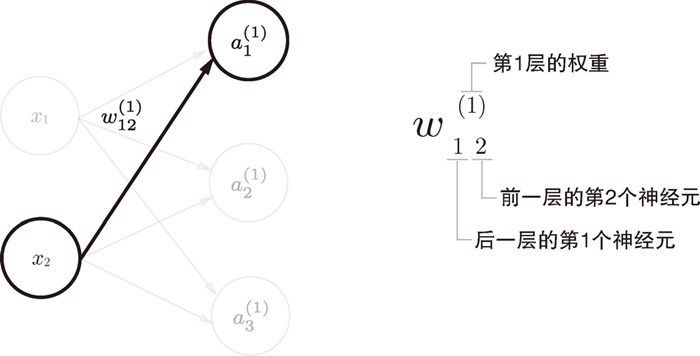
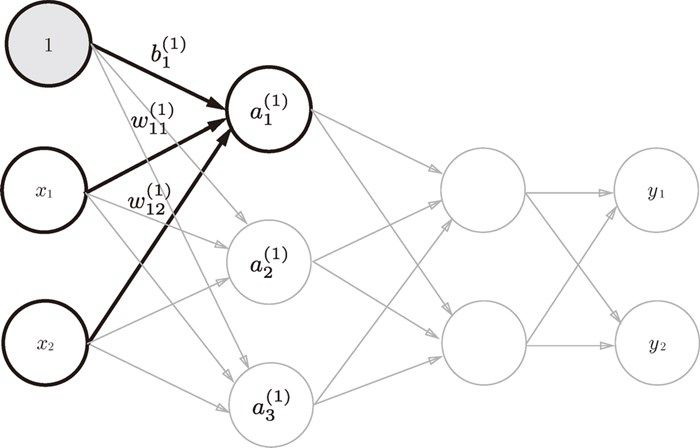
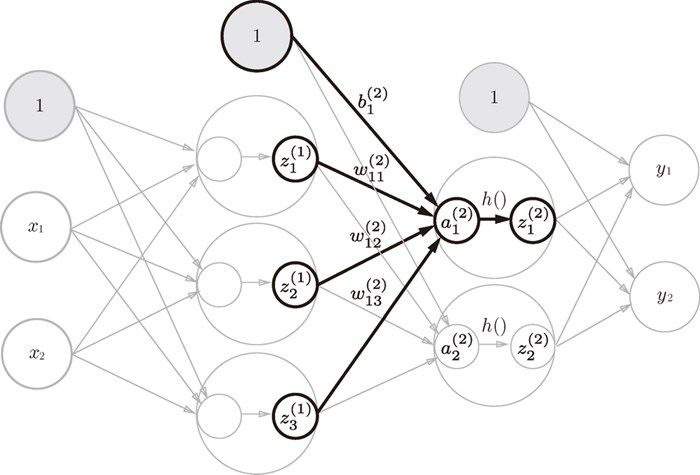
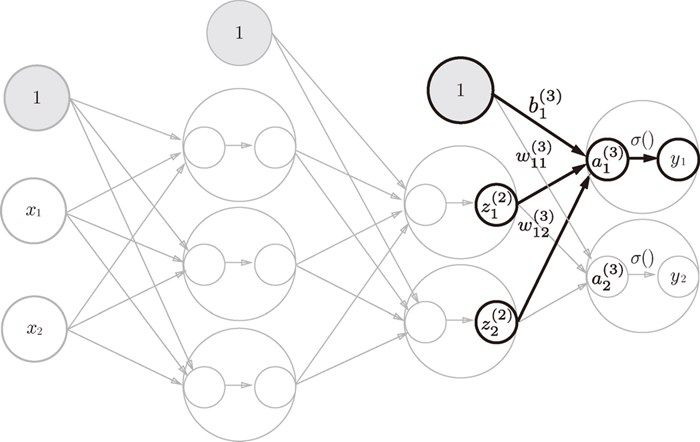
$w_{1\ \ 2}^{(1)}$ 与 $a_1^{(1)}$、$b_1^{(1)}$ 符号引入¶
$a_1^{(1)}$表示第一层第一个神经元的值，$a$左上角的括号中数字表示层数，右小角数字表示当前层数第几个神经元。$b_1^{(1)}$表示第一层第一个神经元的偏置值。$w_{1\ \ 2}^{(1)}$表示表示前一层的第 2 个神经元 $x_2$ 到后一层的第 1 个神经元（对应就是$a_1^{(1)}$）的权重。
对于第一个神经单元的值计算公式：
$$ a_1^{(1)} = w_{1\ 1}^{(1)}x_1\ \ + \ \ w_{1\ 2}^{(1)}x_2\ \ + \ \ b_1^{(1)} $$
推而广之第一层的计算公式：
$$ \mathbf{\mathit{A}}^{(1)} \ \ = \ \ \mathbf{\mathit{X}}\mathbf{\mathit{W}}^{(1)}\ \ \ + \ \ \mathbf{\mathit{B}}^{(1)} $$
其中： $$ \begin{aligned} \mathbf{\mathit{A}}^{(1)} \ \ &= \left\{ \begin{matrix} a_1^{(1)} & a_2^{(2)} & a_3^{(1)} \end{matrix} \right\} \\ \\ \mathbf{\mathit{X}} \ \ &= \left\{ \begin{matrix} x_1 & x_2 \end{matrix} \right\}\\ \\ \mathbf{\mathit{B}}^{(1)} \ \ &= \left\{ \begin{matrix} b_1^{(1)} & b_2^{(1)} & b_3^{(1)} \end{matrix} \right\}\\ \\ \mathbf{\mathit{W}}^{(1)} \ \ &= \left\{ \begin{matrix} w_{1\ 1}^{(1)} & w_{2\ 1}^{(1)} & w_{3\ 1}^{(1)} \\ w_{1\ 2}^{(1)} & w_{2\ 2}^{(1)} & w_{3\ 2}^{(1)} \end{matrix} \right\} \end{aligned} $$
展开后等于：
$$ \begin{aligned} \mathbf{\mathit{A}}^{(1)} \ \ &= \ \ \mathbf{\mathit{X}}\mathbf{\mathit{W}}^{(1)}\ \ \ + \ \ \mathbf{\mathit{B}}^{(1)}\\ &= \left\{ \begin{matrix} x_1 & x_2 \end{matrix} \right\} \times \left\{ \begin{matrix} w_{1\ 1}^{(1)} & w_{2\ 1}^{(1)} & w_{3\ 1}^{(1)} \\ w_{1\ 2}^{(1)} & w_{2\ 2}^{(1)} & w_{3\ 2}^{(1)} \end{matrix} \right\} + \left\{ \begin{matrix} b_1^{(1)} & b_2^{(1)} & b_3^{(1)} \end{matrix} \right\} \end{aligned} $$
### 传输层到第一层的信号传递实现
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2 , 0.3]) # 偏置的数量取决于后一层的神经元的数量
print(X.shape)
print(W1.shape)
print(B1.shape)
A1 = np.dot(X, W1) + B1
A1
(2,) (2, 3) (3,)
array([0.3, 0.7, 1.1])
Z1 = sigmoid(A1) # 激活函数处理
Z1
array([0.57444252, 0.66818777, 0.75026011])
带激活函数的输入层到第一层的信号传递：
## 第1层到第2层的信号传递
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2 = np.dot(Z1, W2) + B2
A2
(3,) (3, 2) (2,)
array([0.51615984, 1.21402696])
Z2 = sigmoid(A2)
Z2
array([0.62624937, 0.7710107 ])
第1 层到第2 层的示意图：
## 第2层到输出层的信号传递实现
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
print(A3)
Y = identity_function(A3) # 或者 Y = A3
[0.31682708 0.69627909]
第二次到输出层的示意图：
注意此时输出层的激活函数用 $\sigma()$（读sigma)表示。不同于隐藏层的激活 $h()$。另外使用恒等函数$identity_functon()$作为了激活函数，目的是为了将输入按照原样输出。
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x): # forward（前向）一词，它表示的是从输入到输出方向的传递处理
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
y # [ 0.31682708 0.69627909]
array([0.31682708, 0.69627909])
输出层的设计¶
神经网络可以用来解决 分类问题和 回归问题 上（即定性问题与定量问题）。分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性 的问题就是分类问题。而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题（类似“57.4kg”这样的预测）。
一般而言，回归问题用恒等函数，分类问题用 softmax 函数。